Sayo MathsPractice & Assess

Sign in Get Started

Euclidean Geometry Cheat Sheet

Struggling to remember the exact wording for geometry proofs? This tool is designed to help HKDSE Mathematics students instantly find and review geometry reasons covered in the syllabus.

Lines

12

adj. $\angle$s on st. line

$adj. $\angle$s on st. line$

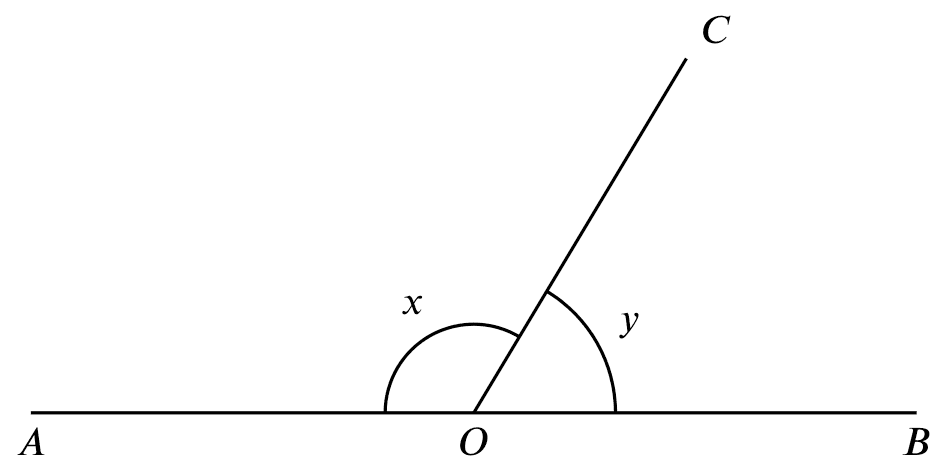
If

If AOB is a straight line,

Then

$x+y=180^{\circ}$

adj. $\angle$s supp.

$adj. $\angle$s supp.$

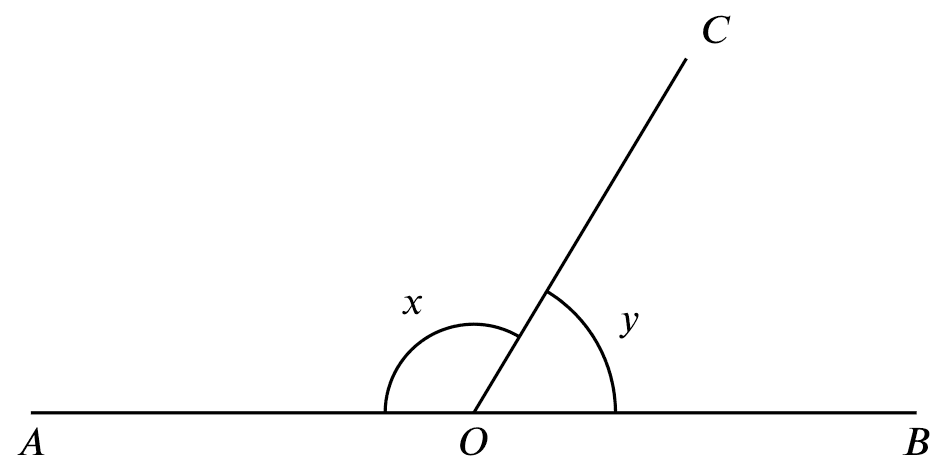
If

If $x+y=180^{\circ}$

Then

AOB is a straight line.

$\angle$s at a pt.

$$\angle$s at a pt.$

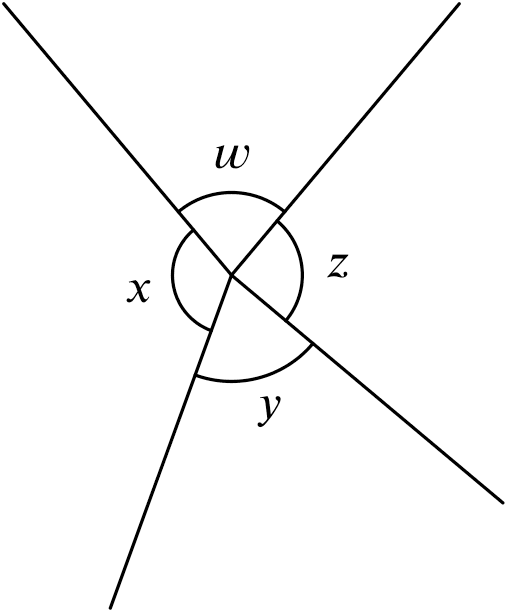
$w+x+y+z=360^{\circ}$

vert. opp. $\angle$s

$vert. opp. $\angle$s$

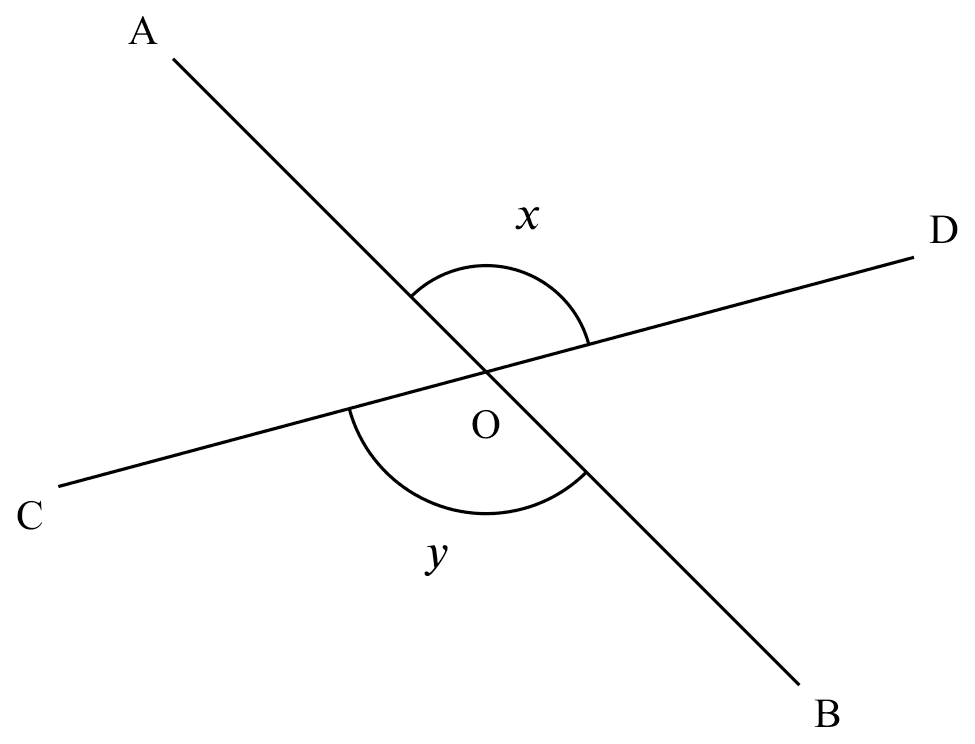
If

If lines AB and CD meet at O,

Then

$x = y$

corr. $\angle$s, AB$\parallel$CD

$corr. $\angle$s, AB$\parallel$CD$

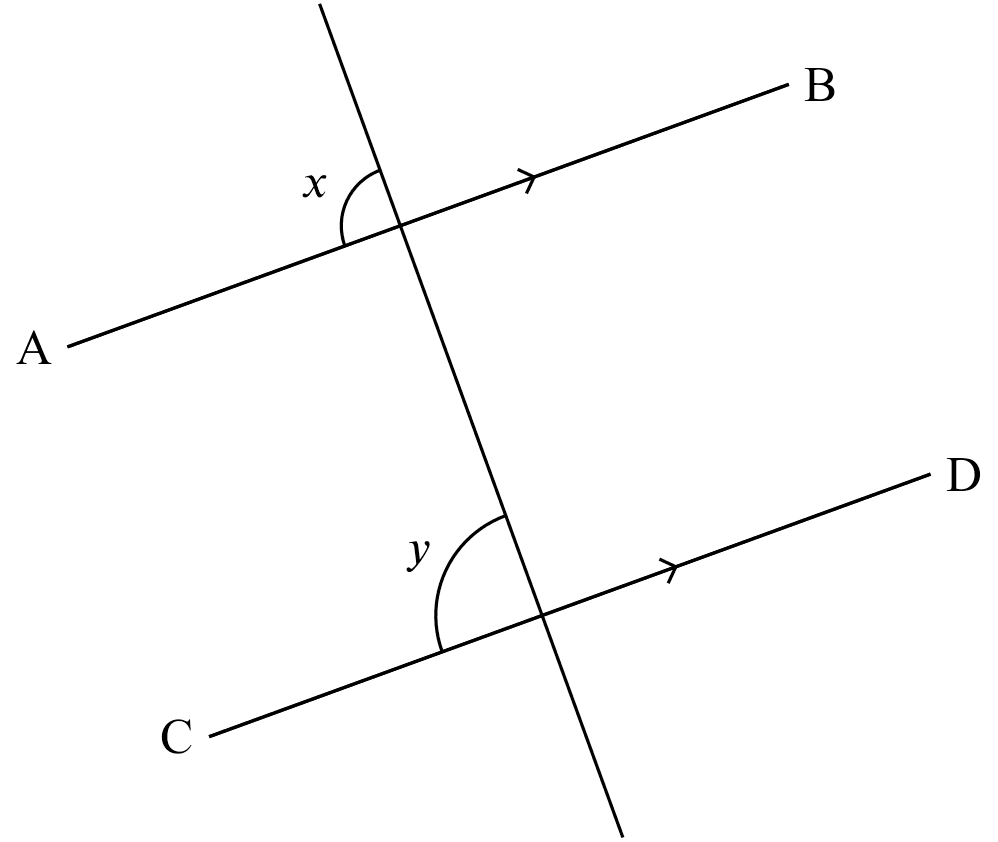
If

If $AB \parallel CD$,

Then

$x = y$

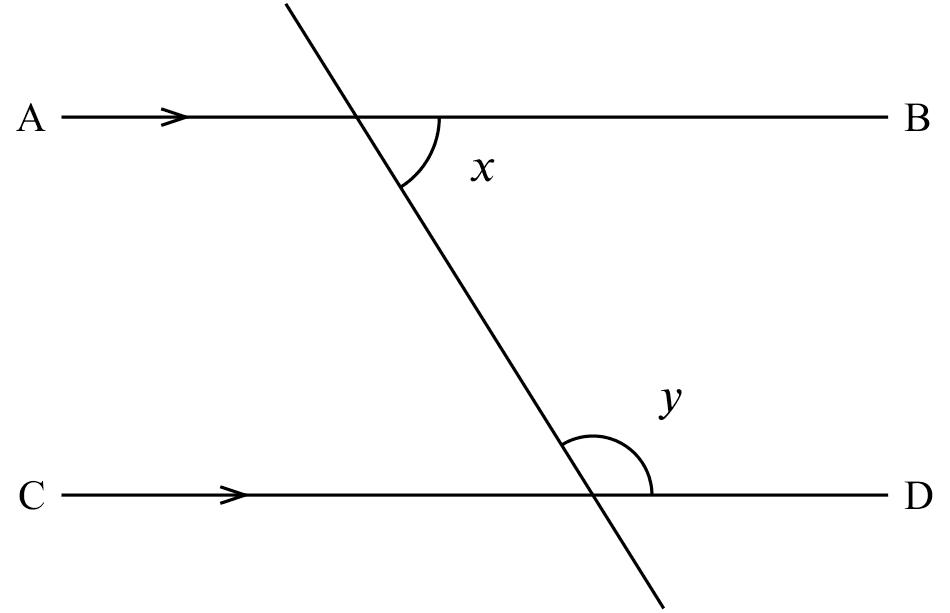
alt. $\angle$s, AB$\parallel$CD

$alt. $\angle$s, AB$\parallel$CD$

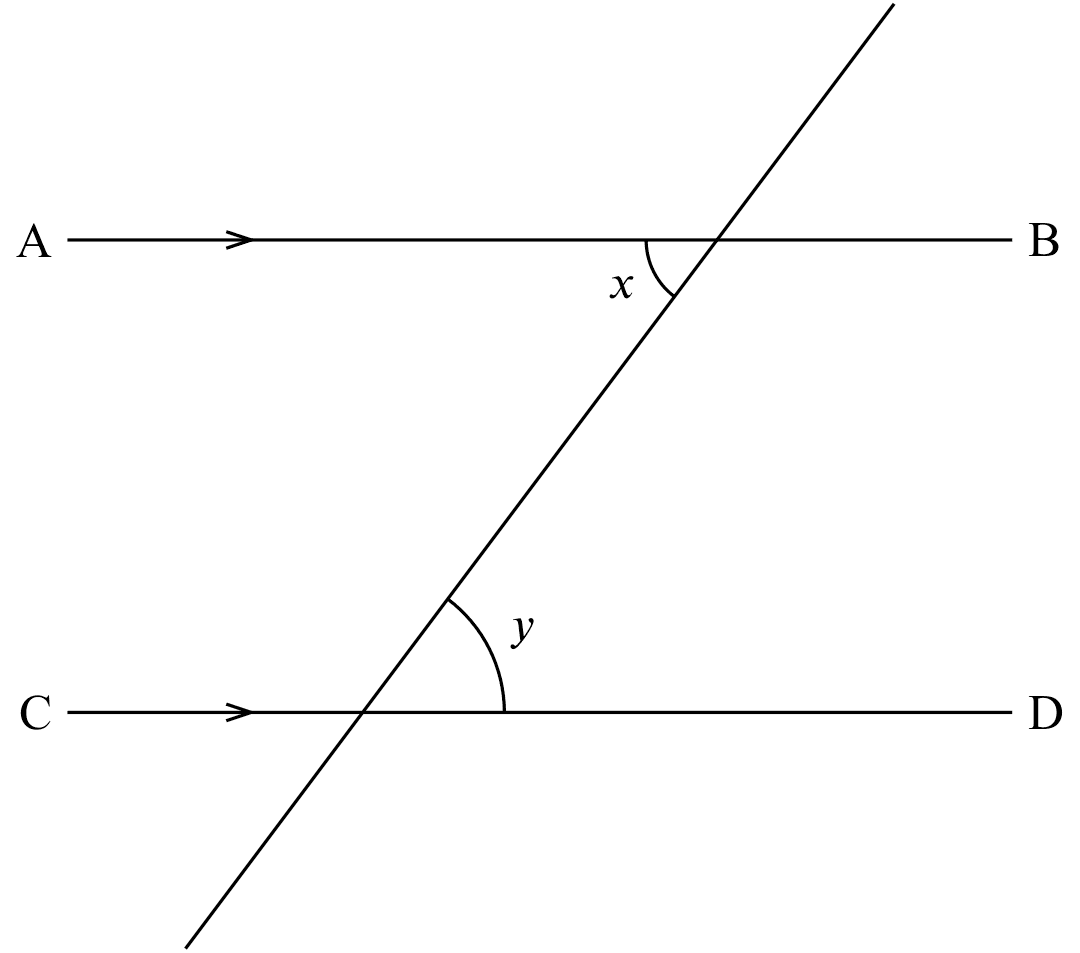
If

If $AB \parallel CD$,

Then

$x = y$

int. $\angle$s, AB$\parallel$CD

$int. $\angle$s, AB$\parallel$CD$

If

If $AB \parallel CD$,

Then

$x+y=180^{\circ}$

corr. $\angle$s equal

$corr. $\angle$s equal$

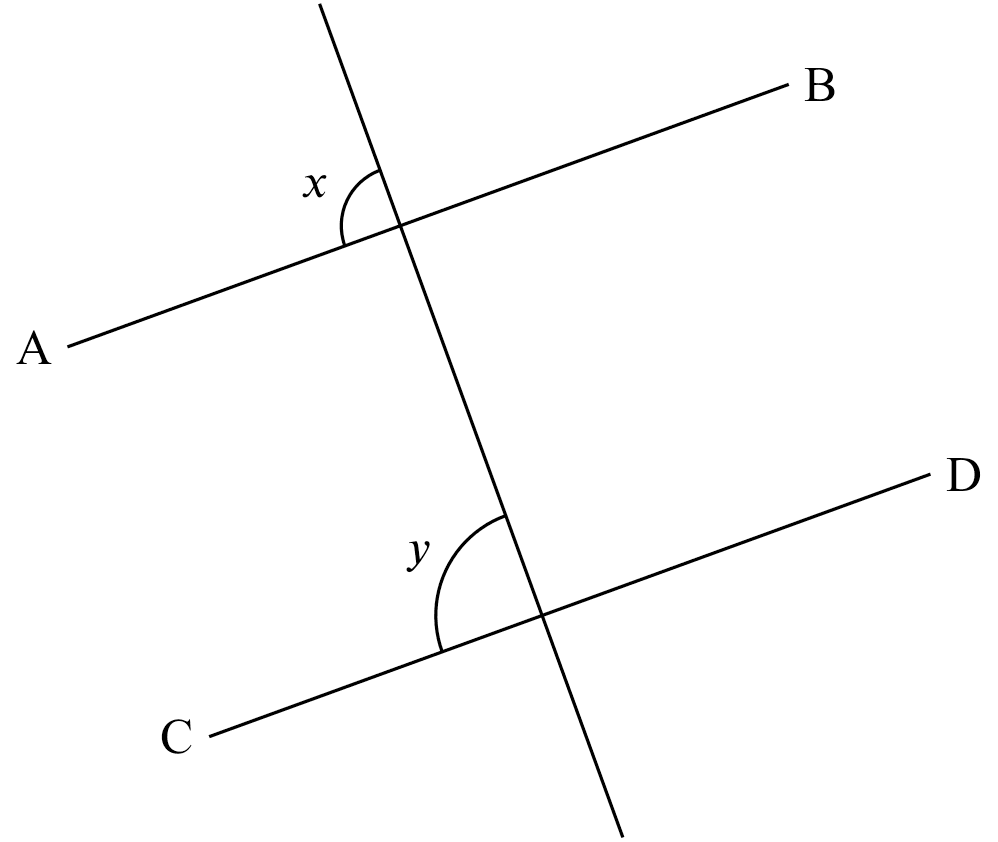
If

If $x = y$,

Then

$AB \parallel CD$

alt. $\angle$s equal

$alt. $\angle$s equal$

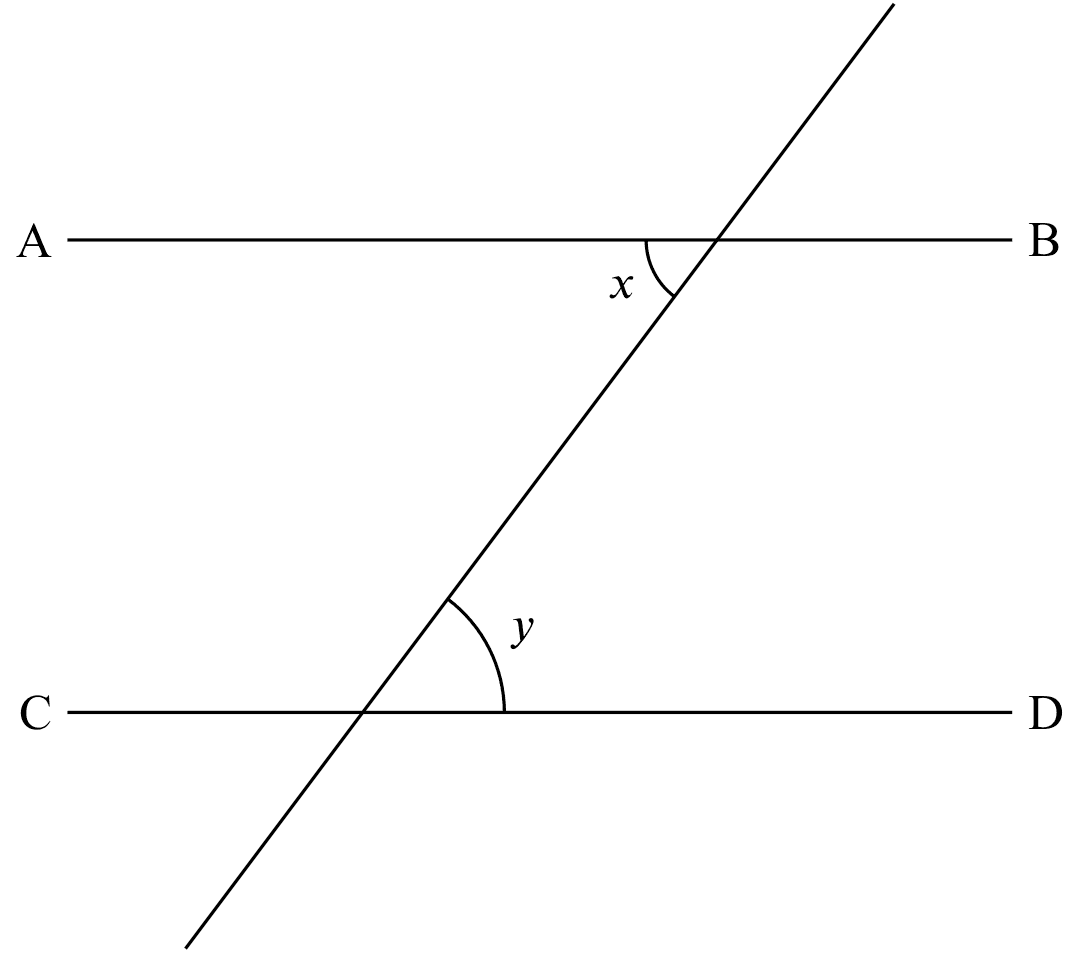
If

If $x = y$,

Then

$AB \parallel CD$

int. $\angle$s supp.

$int. $\angle$s supp.$

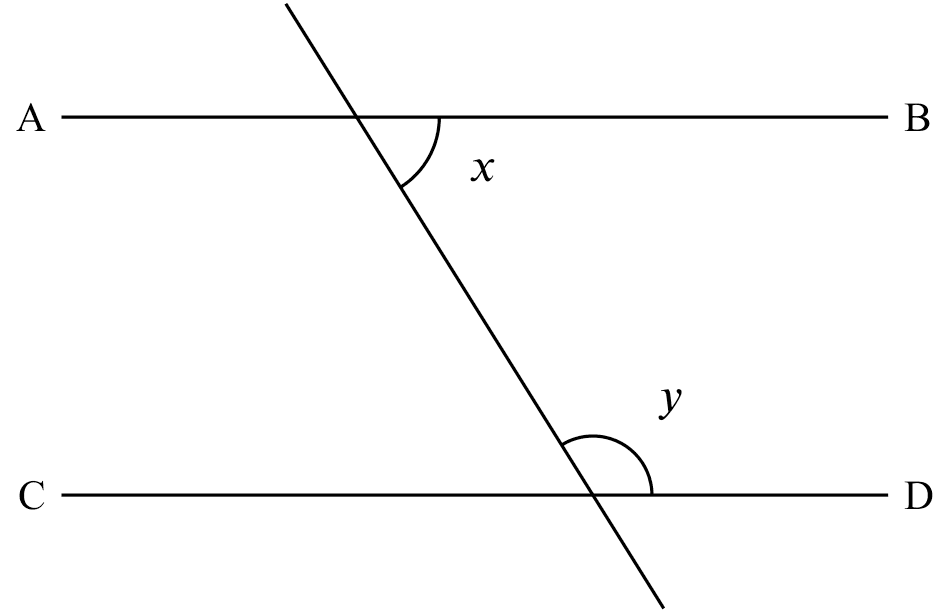
If

If $x+y=180^{\circ}$

Then

$AB \parallel CD$

mid-pt. theorem

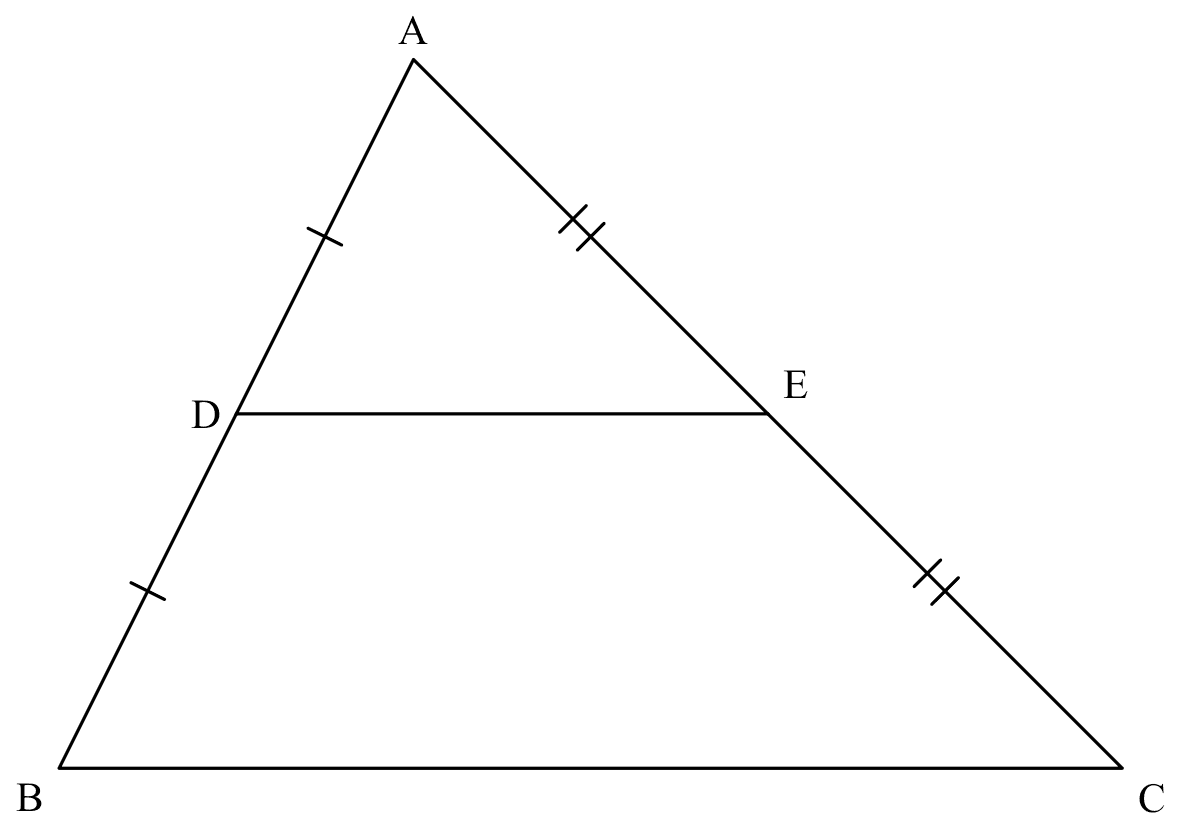
mid-pt. theorem

If

If $AD=DB$ and $AE=EC$ (D,E midpoints of AB, AC),

Then

$DE \parallel BC$

$BC = 2DE$

intercept theorem

intercept theorem

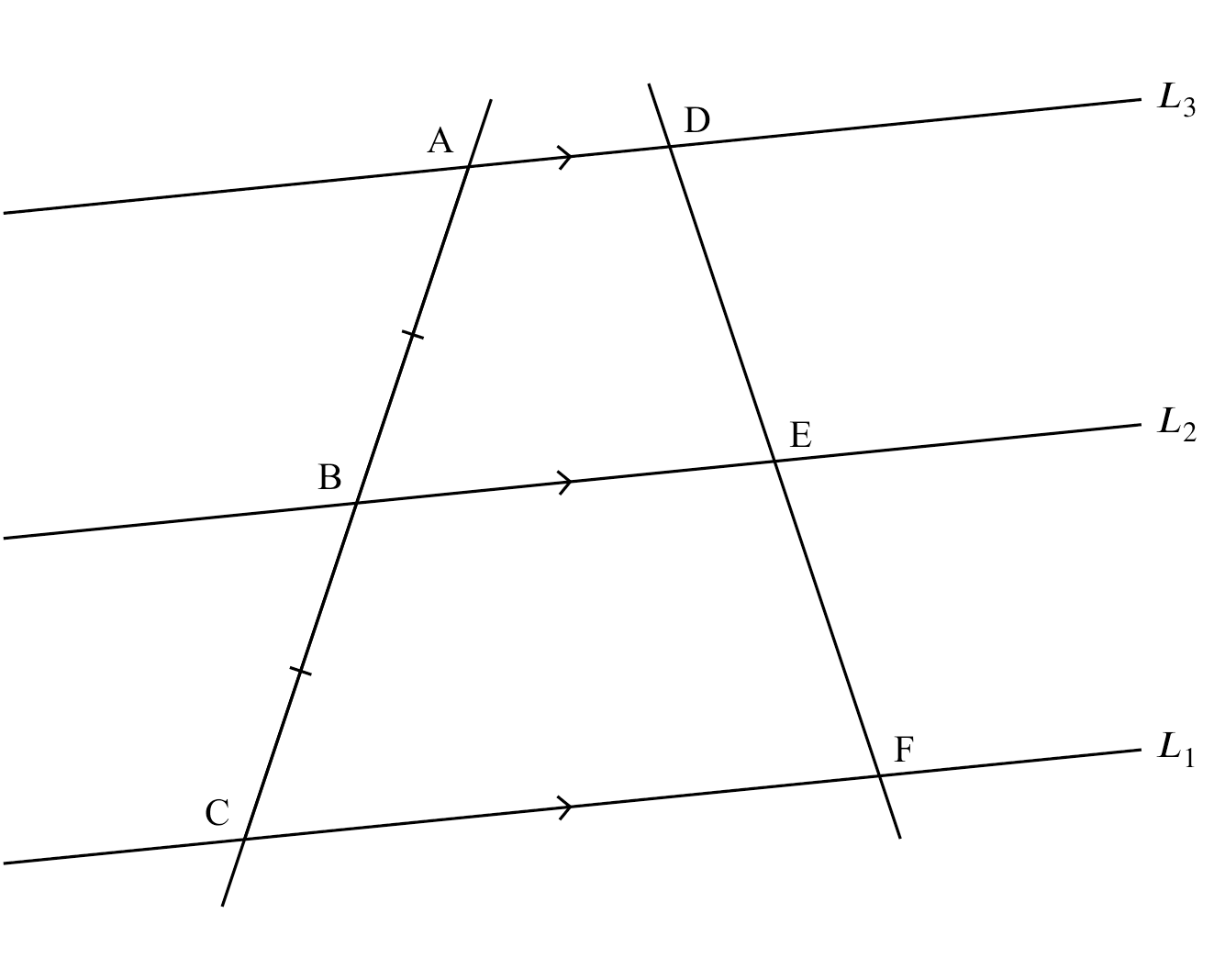
If

If $AD \parallel BE \parallel CF$ and $AB = BC$,

Then

$DE = EF$

Triangles

22

$\angle$ sum of $\triangle$

$\angle$ sum of $\triangle$

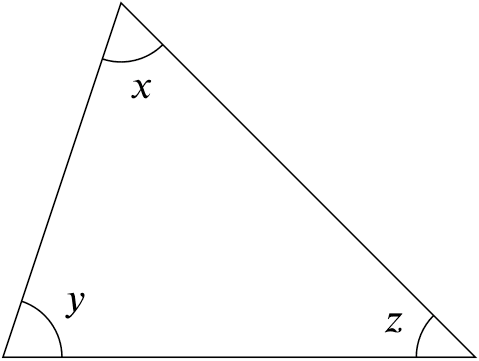
$x+y+z=180^{\circ}$

ext. $\angle$ of $\triangle$

$ext. $\angle$ of $\triangle$$

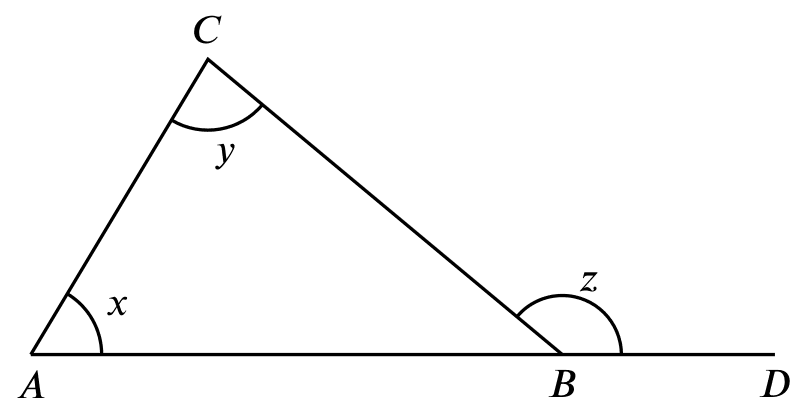
$x+y=z$

SAS

SAS

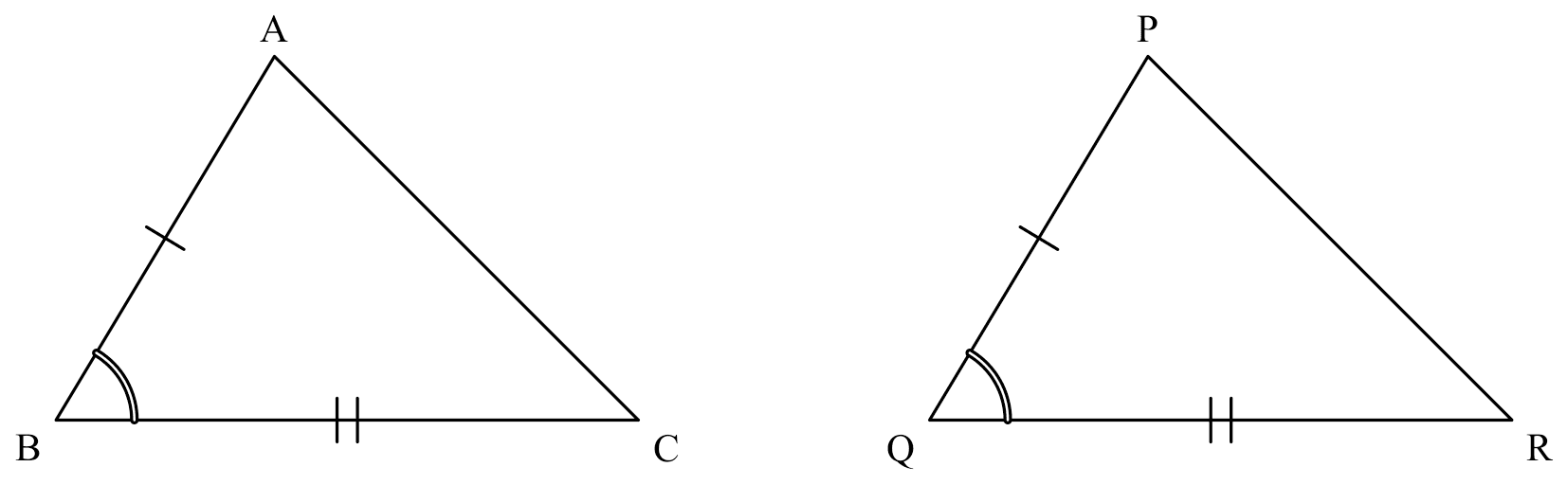
If

If $AB=PQ$, $\angle ABC=\angle PQR$, $BC=QR$,

Then

$\triangle ABC \cong \triangle PQR$

SSS

SSS

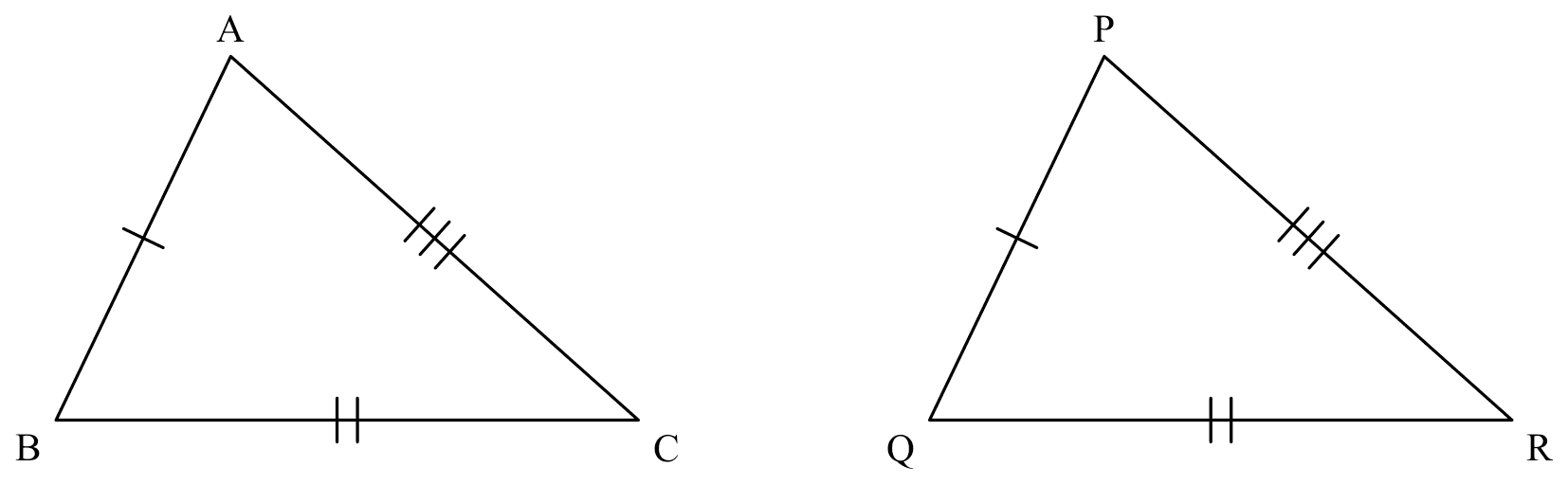
If

If $AB=PQ$, $BC=QR$, $AC=PR$,

Then

$\triangle ABC \cong \triangle PQR$

ASA

ASA

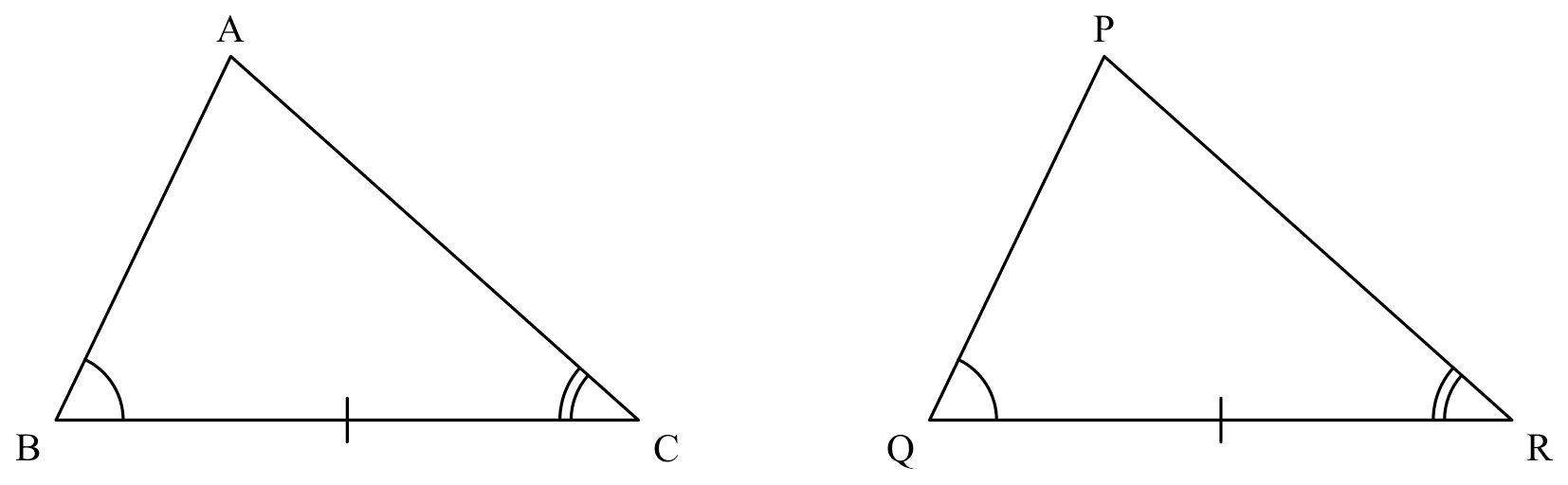
If

If $\angle ABC=\angle PQR$, $BC=QR$, $\angle ACB=\angle PRQ$,

Then

$\triangle ABC \cong \triangle PQR$

AAS

AAS

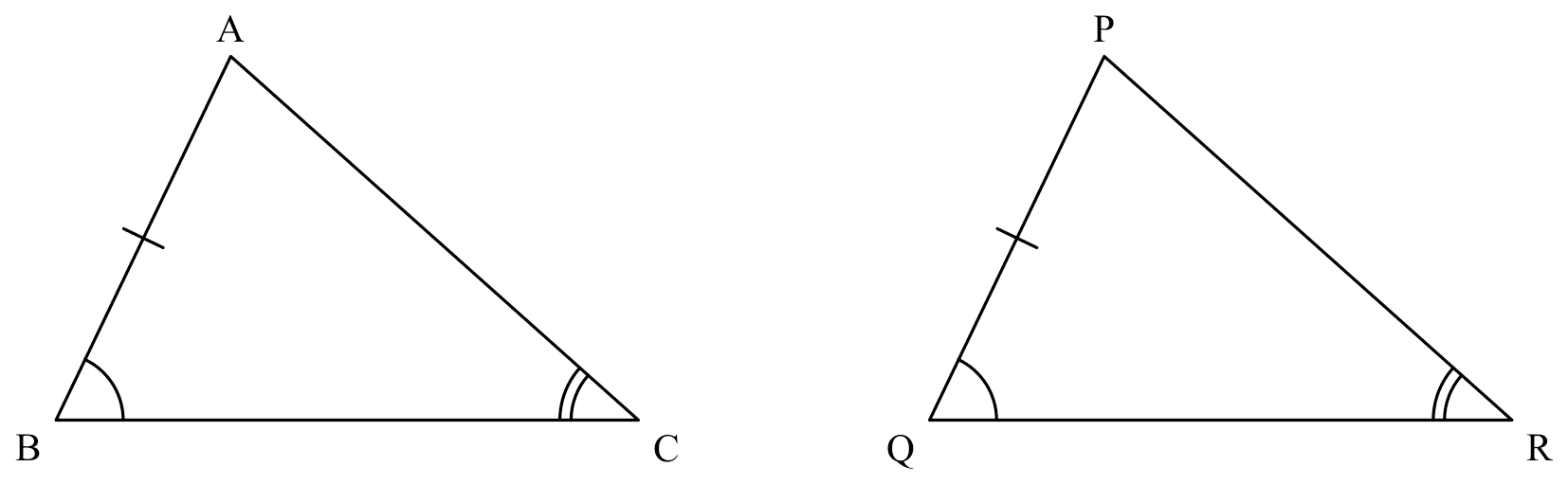
If

If $\angle ABC=\angle PQR$, $\angle ACB=\angle PRQ$, $AB=PQ$,

Then

$\triangle ABC \cong \triangle PQR$

RHS

RHS

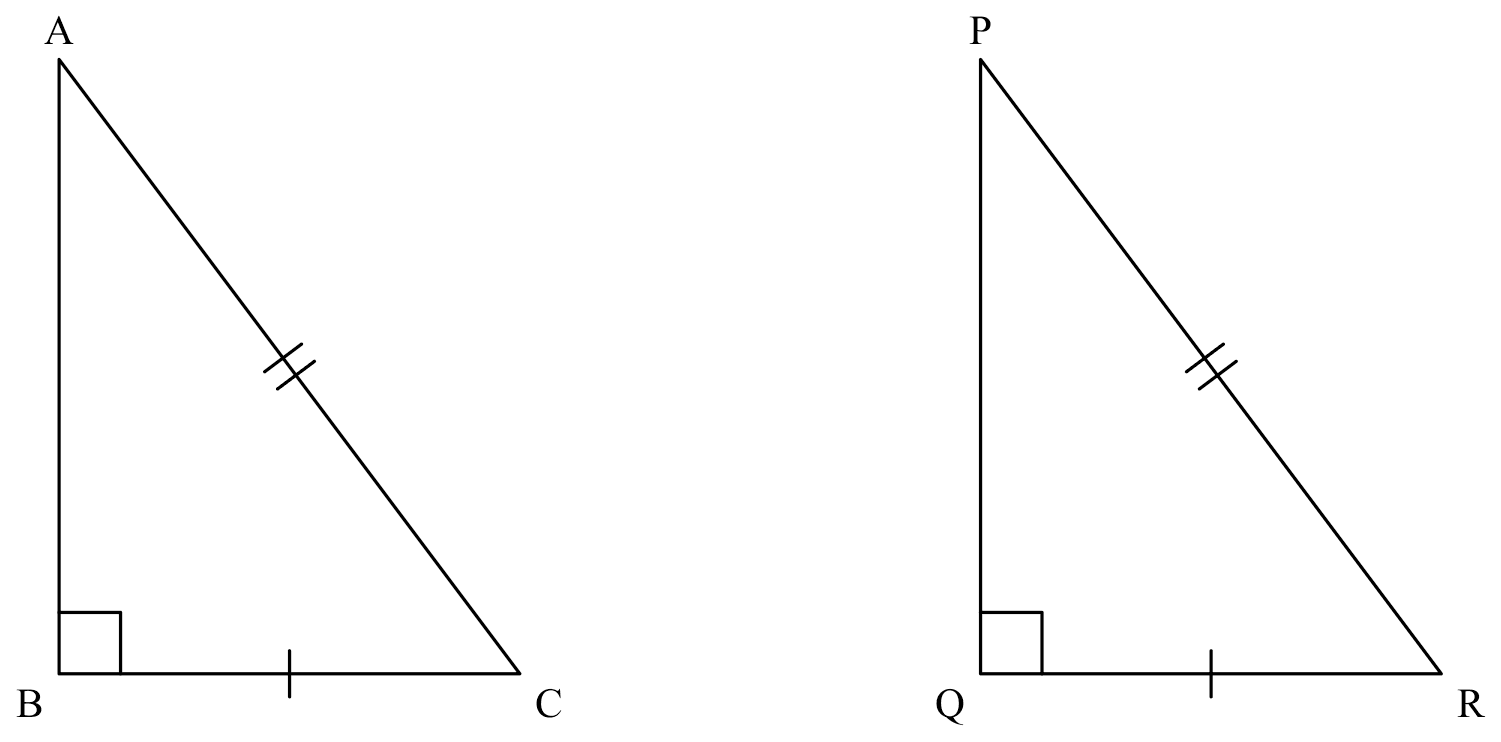
If

If $\angle ABC=\angle PQR=90^{\circ}$, $AC=PR$ (hypotenuse), $BC=QR$ (side),

Then

$\triangle ABC \cong \triangle PQR$

AAA

AAA

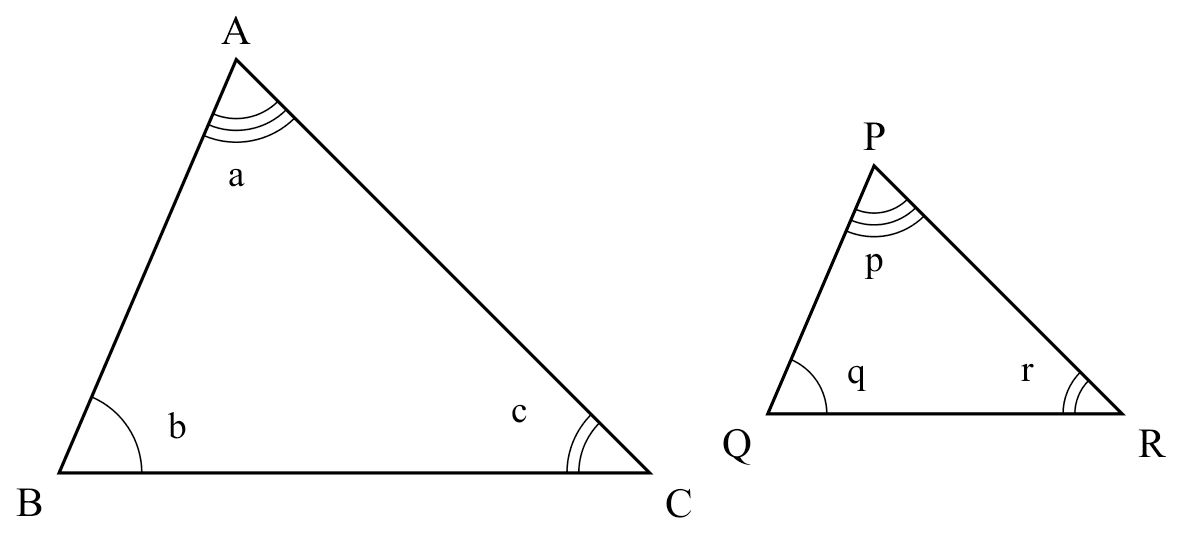
If

If $a=p$, $b=q$, $c=r$,

Then

$\triangle ABC \cong \triangle PQR$

AA

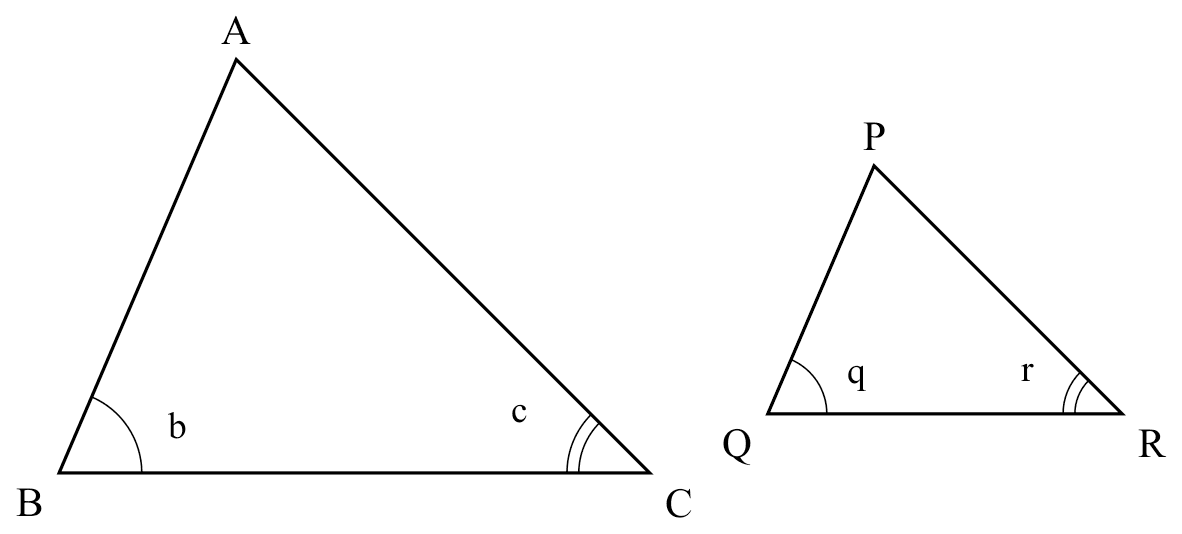
If

If $b=q$, $c=r$,

Then

$\triangle ABC \sim \triangle PQR$

3 sides proportional

3 sides proportional

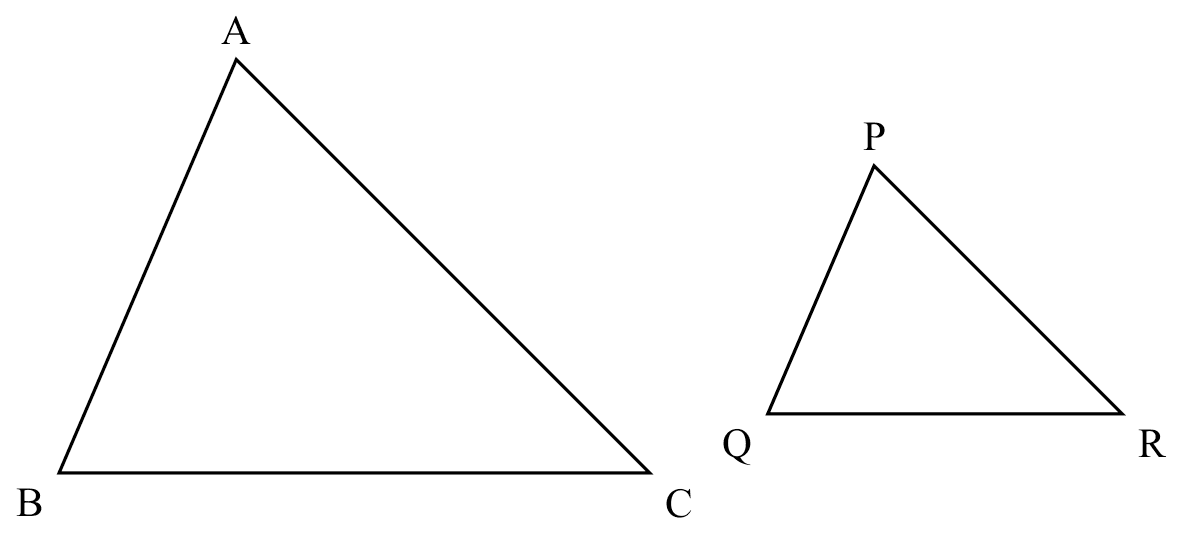
If

If $\frac{AB}{PQ}= \frac{BC}{QR}= \frac{AC}{PR}$,

Then

$\triangle ABC \sim \triangle PQR$

ratio of 2 sides, inc. $\angle$

$ratio of 2 sides, inc. $\angle$$

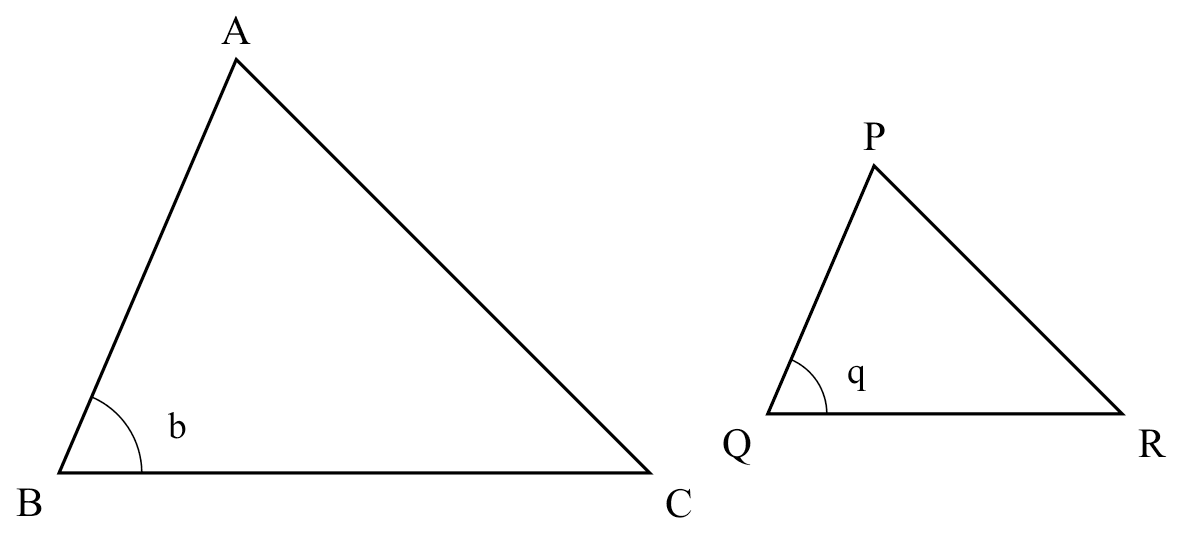
If

If $b=q$ and $\frac{AB}{PQ}= \frac{BC}{QR}$,

Then

$\triangle ABC \sim \triangle PQR$

corr. $\angle$s, $\cong$ $\triangle$s

$corr. $\angle$s, $\cong$ $\triangle$s$

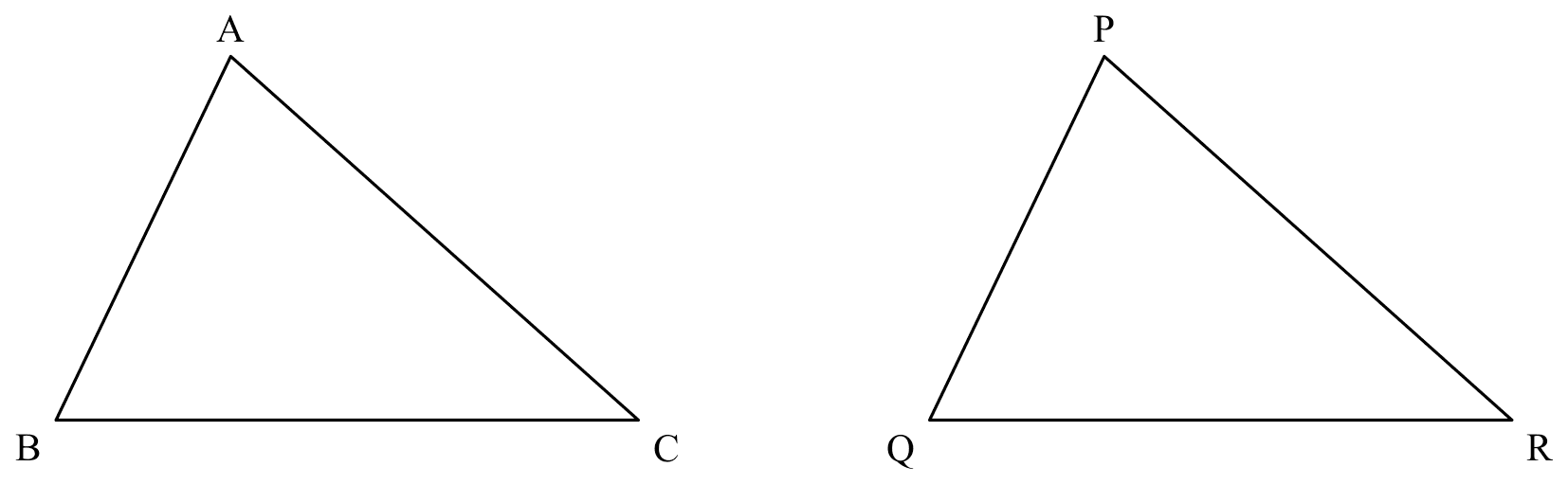
If

If $\triangle ABC \cong \triangle PQR$,

Then

$\angle ABC=\angle PQR$

$\angle BCA=\angle QRP$

$\angle ACB=\angle PRQ$

corr. sides, $\cong$ $\triangle$s

$corr. sides, $\cong$ $\triangle$s$

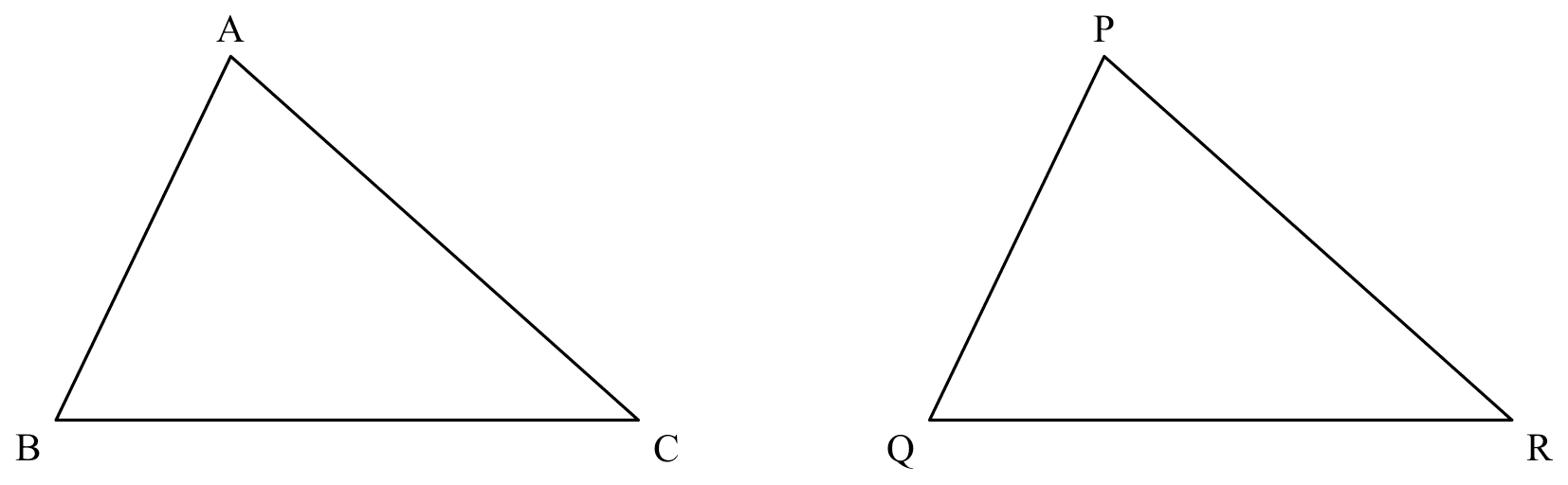
If

If $\triangle ABC \cong \triangle PQR$,

Then

$AB=PQ$

$BC=QR$

$AC=PR$

corr. $\angle$s, $\sim$ $\triangle$s

$corr. $\angle$s, $\sim$ $\triangle$s$

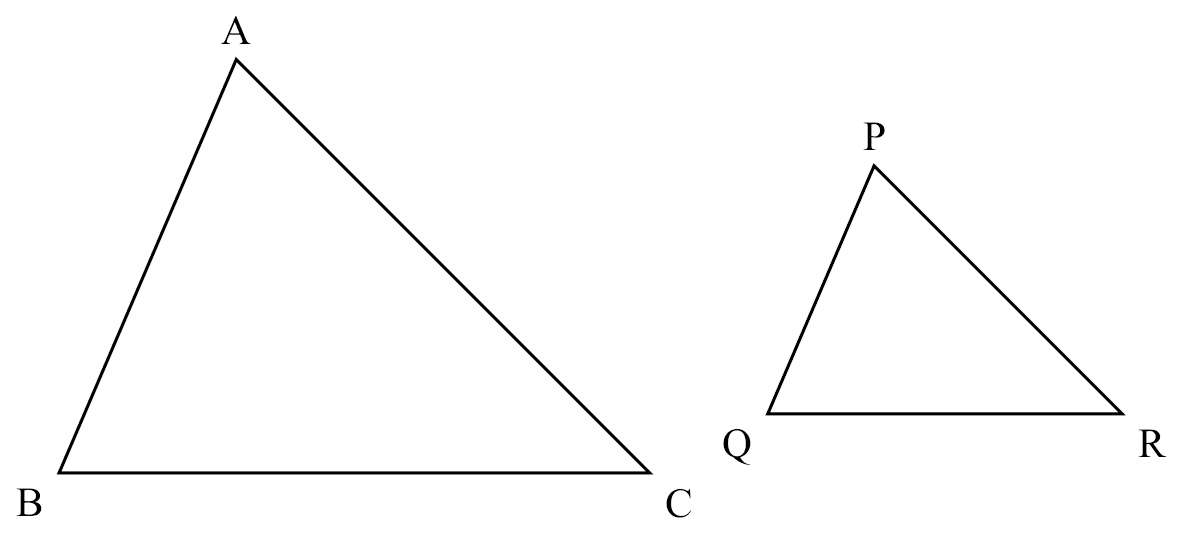
If

If $\triangle ABC \sim \triangle PQR$,

Then

$\angle ABC=\angle PQR$

$\angle BCA=\angle QRP$

$\angle ACB=\angle PRQ$

corr. sides, $\sim$ $\triangle$s

$corr. sides, $\sim$ $\triangle$s$

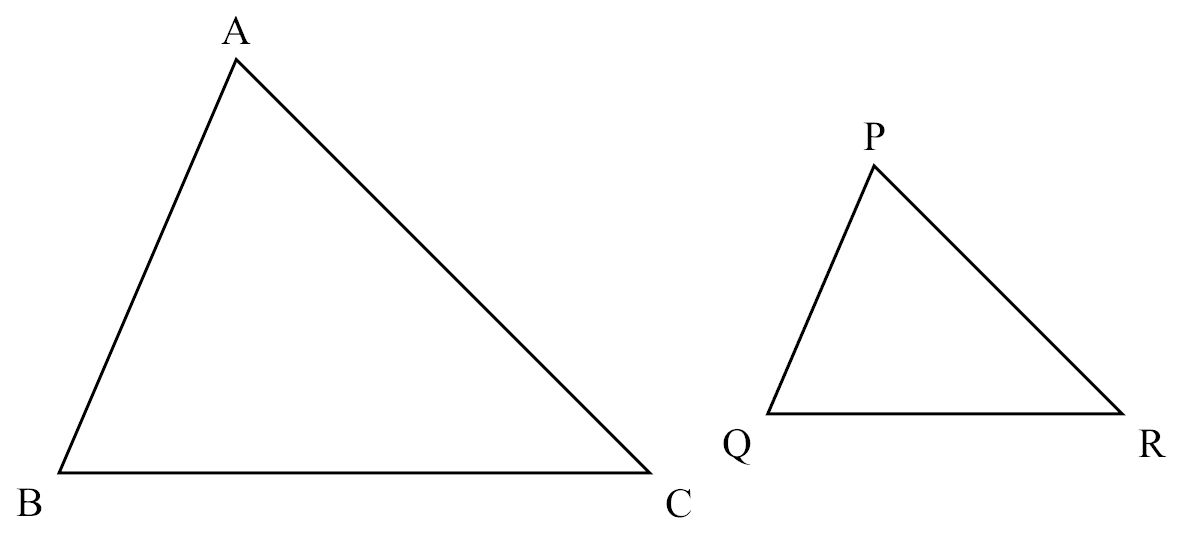
If

If $\triangle ABC \sim \triangle PQR$,

Then

$\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}$

base $\angle$s, isos. $\triangle$

$base $\angle$s, isos. $\triangle$$

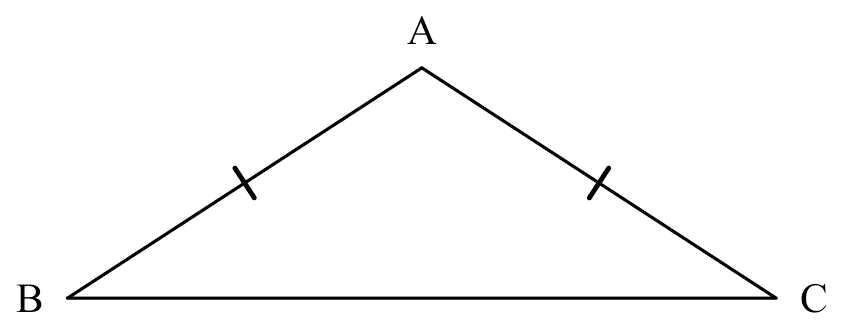
If

If $AB = BC$,

Then

$\angle ABC = \angle ACB$

sides opp. equal $\angle$s

$sides opp. equal $\angle$s$

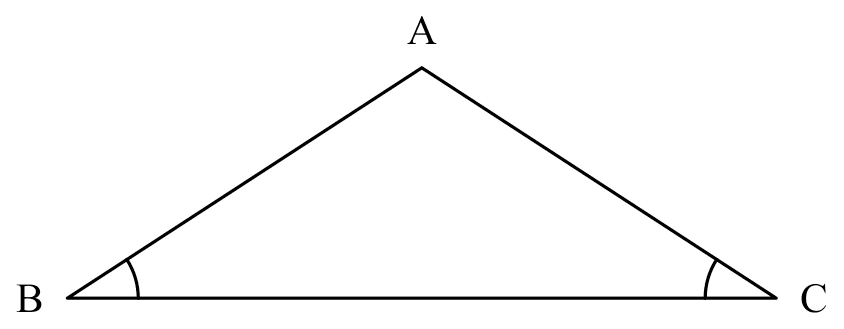
If

If $\angle ABC = \angle ACB$,

Then

$AB = AC$

property of isos. $\triangle$

$property of isos. $\triangle$$

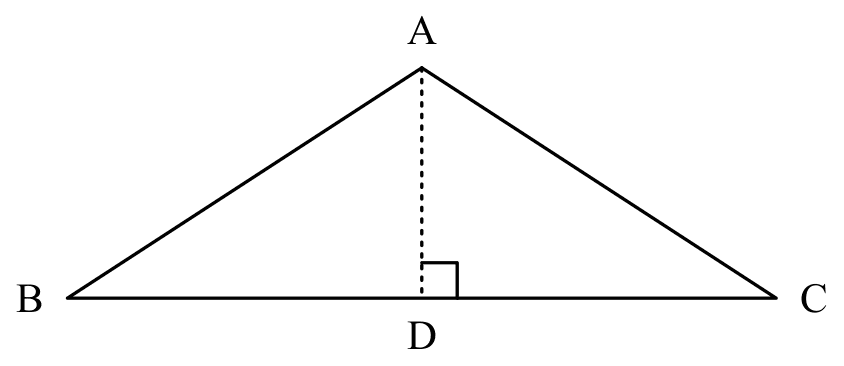
If

If $\triangle ABC$ is isosceles ($AB = AC$),

Then

$\angle BAD=\angle CAD$

$BD=CD$

$AD \perp BC$

property of equil. $\triangle$

$property of equil. $\triangle$$

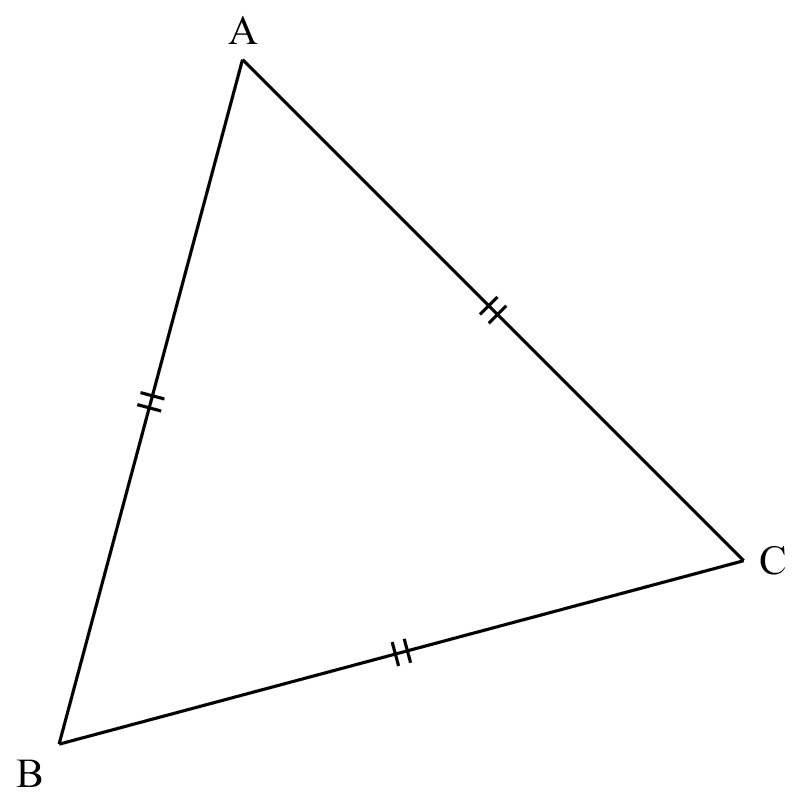
If

If $\triangle ABC$ is equilateral ($AB=BC=AC$),

Then

$\angle ABC = \angle ACB = \angle BAC = 60^{\circ}$

pyth. thm

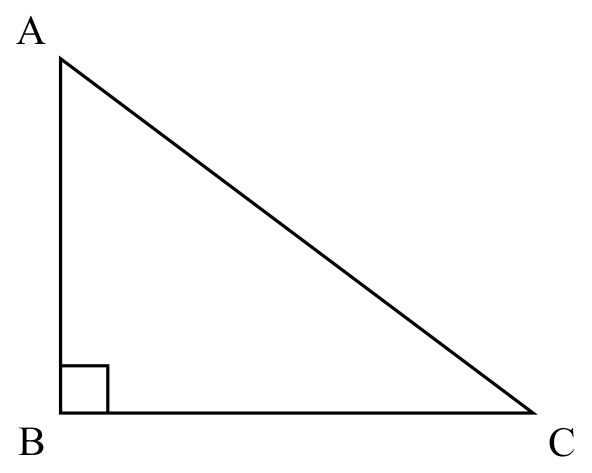
pyth. thm

If

If $\triangle ABC$ is right-angled (at B),

Then

$AB^{2} + BC^{2} = AC^{2}$

converse of pyth. thm

converse of pyth. thm

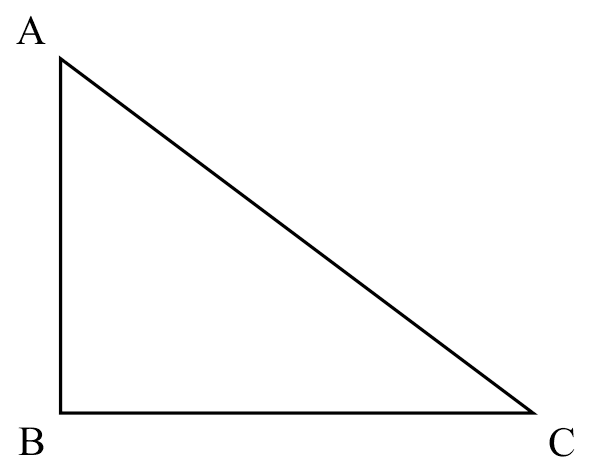
If

If $AB^{2} + BC^{2} = AC^{2}$,

Then

$\triangle ABC$ is right-angled and $\angle ABC = 90^{\circ}$

triangle inequality

triangle inequality

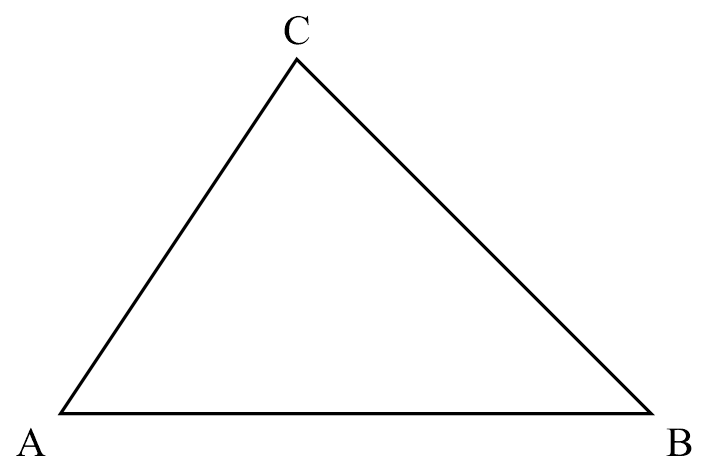
$AB+AC>BC$

$AB+BC>AC$

$AC+BC>AB$

Quadrilaterals

15

$\angle$ sum of polygon

$$\angle$ sum of polygon$

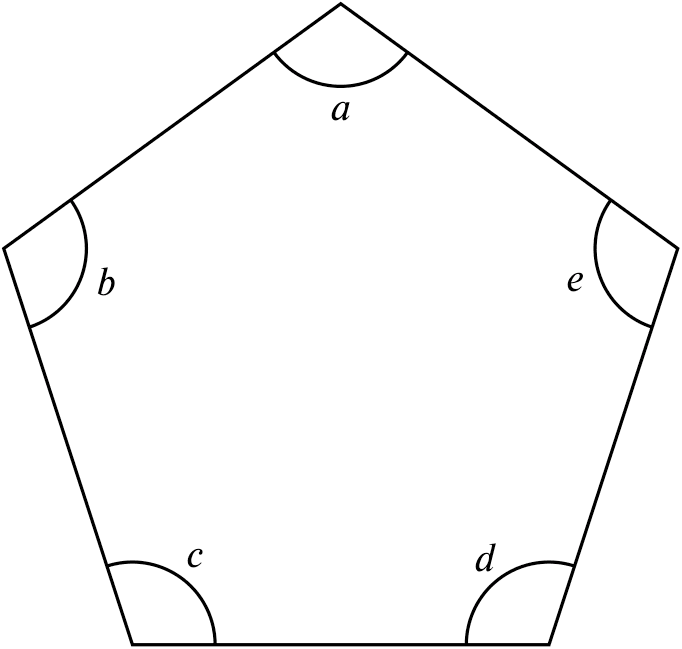
$\text{Sum of interior angles}= (n-2)\times180^{\circ}$

e.g. sum of interior angles of pentagon $(5-2)\times180^{\circ}=540^{\circ}$

$a+b+c+d+e=540^{\circ}$

sum of ext. $\angle$s of polygon

$sum of ext. $\angle$s of polygon$

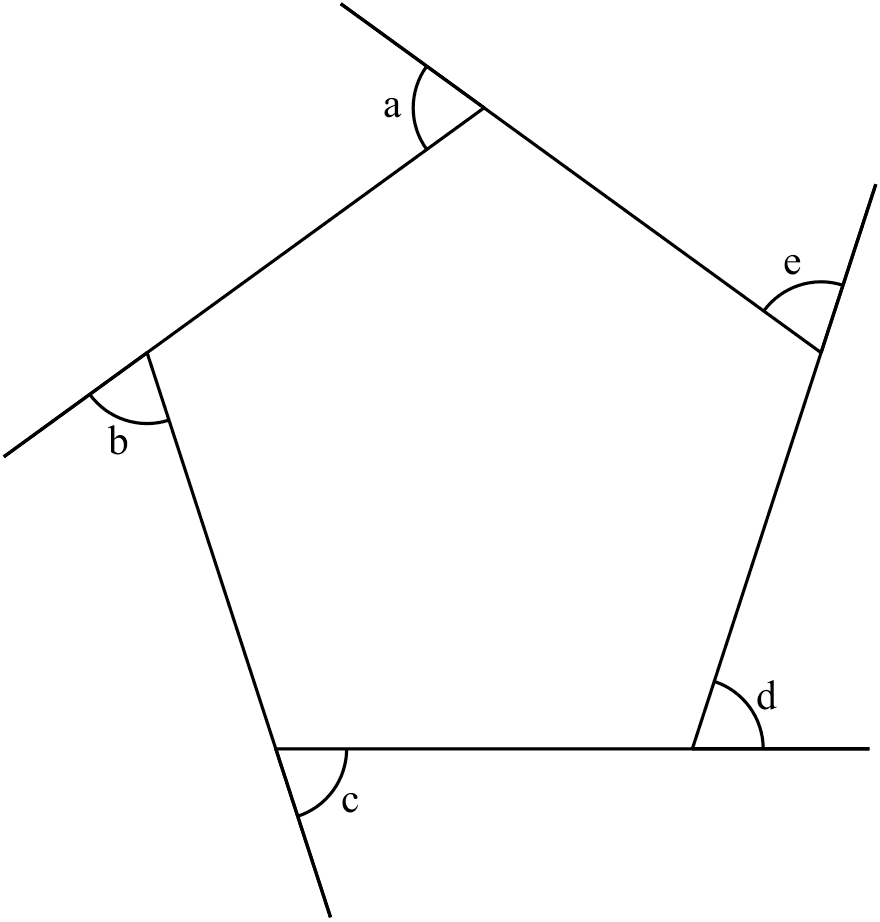
$\text{Sum of exterior angles}= 360^{\circ}$

e.g. $a+b+c+d+e=360^{\circ}$

opp. sides of $\parallel$gram

$opp. sides of $\parallel$gram$

If

If $ABCD$ is a parallelogram,

Then

$AB = DC$

$AD = BC$

opp. $\angle$s of $\parallel$gram

$opp. $\angle$s of $\parallel$gram$

If

If $ABCD$ is a parallelogram,

Then

$\angle DAB = \angle BCD$

$\angle ADB = \angle ABC$

diags. of $\parallel$gram

$diags. of $\parallel$gram$

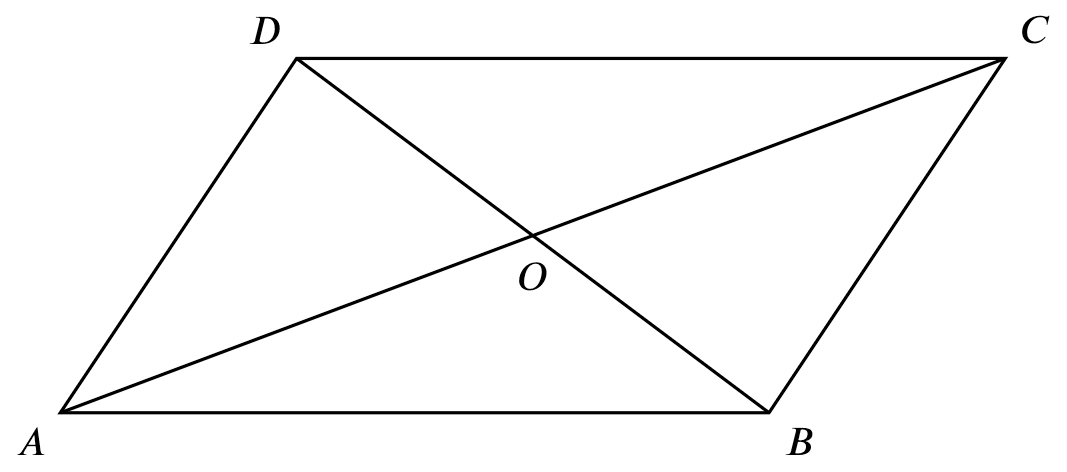
If

If $ABCD$ is a parallelogram,

Then

$OD=OB$

$OA=OC$

diagonals bisect area of $\parallel$gram

$diagonals bisect area of $\parallel$gram$

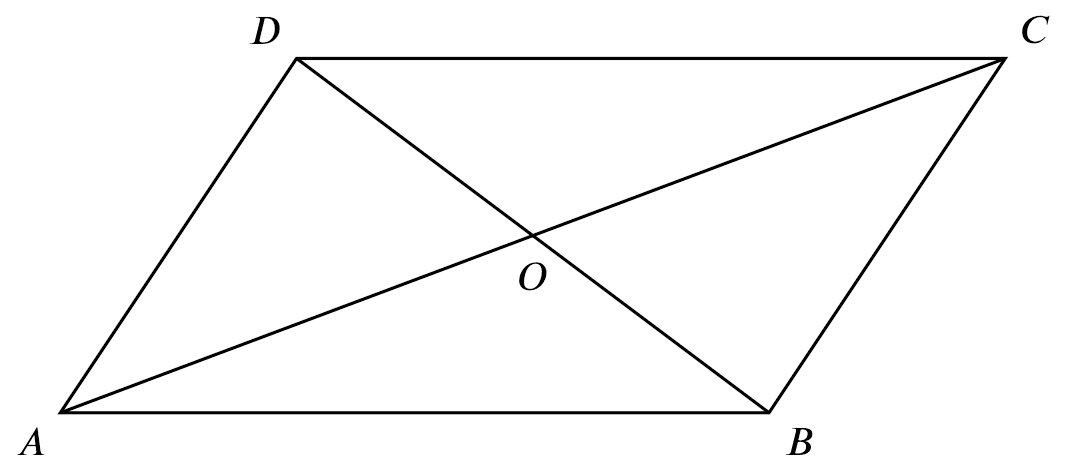
If

If $ABCD$ is a parallelogram,

Then

$\text{Area of }\triangle ACD = \text{Area of }\triangle ACB$

$\text{Area of }\triangle ABD = \text{Area of }\triangle CBD$

opp. sides equal

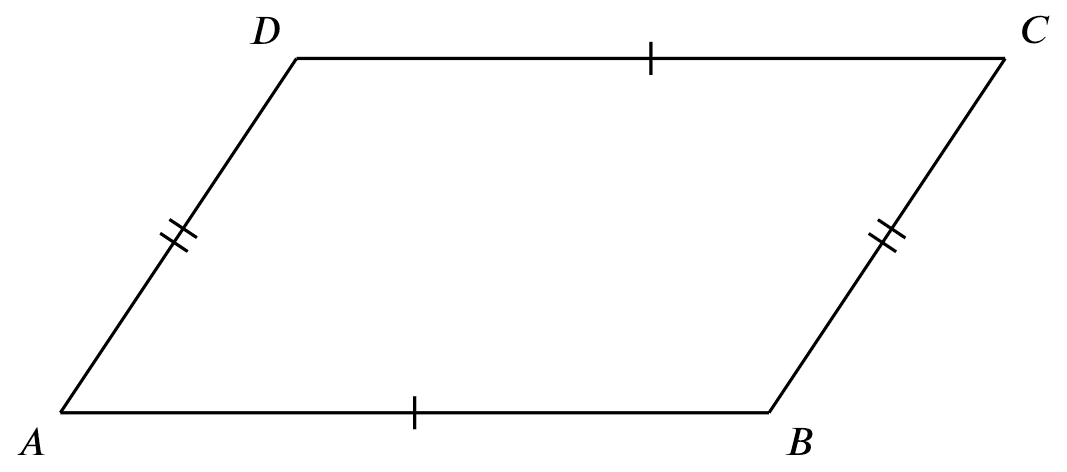
opp. sides equal

If

If $AB = DC$ and $AD = BC$,

Then

$ABCD$ is a parallelogram

opp. $\angle$s equal

$opp. $\angle$s equal$

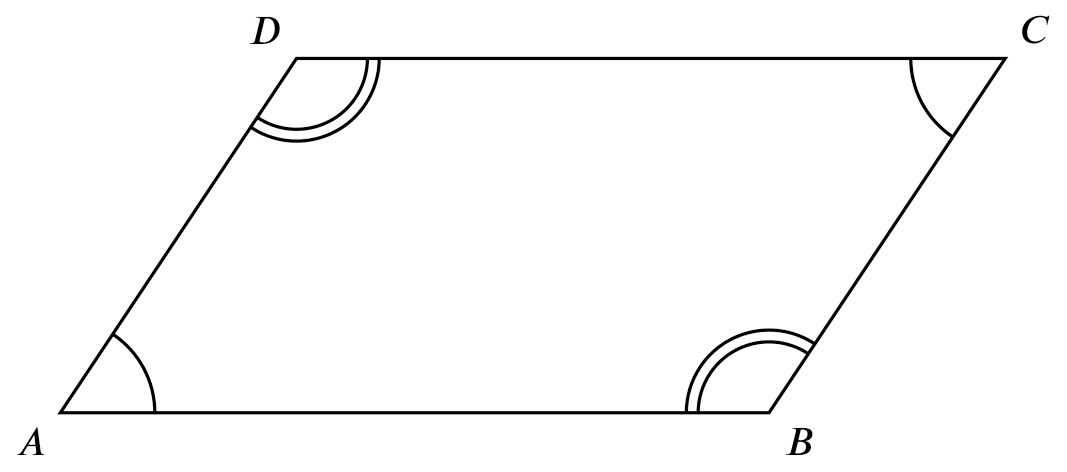
If

If $\angle ADC=\angle ABC$ and $\angle DAB=\angle DCB$,

Then

$ABCD$ is a parallelogram

diags. bisect each other

diags. bisect each other

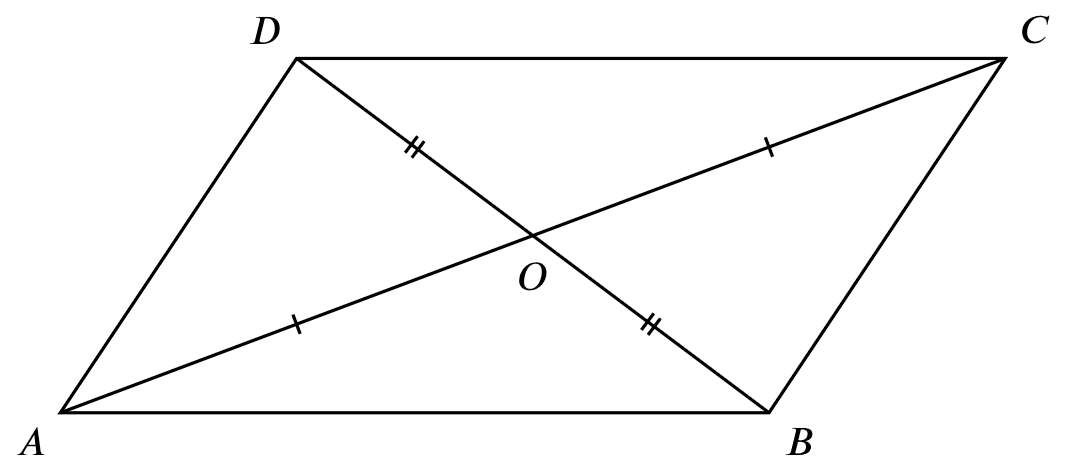
If

If $OA = OC$ and $OD = OB$,

Then

$ABCD$ is a parallelogram

opp. sides equal and $\parallel$

$opp. sides equal and $\parallel$$

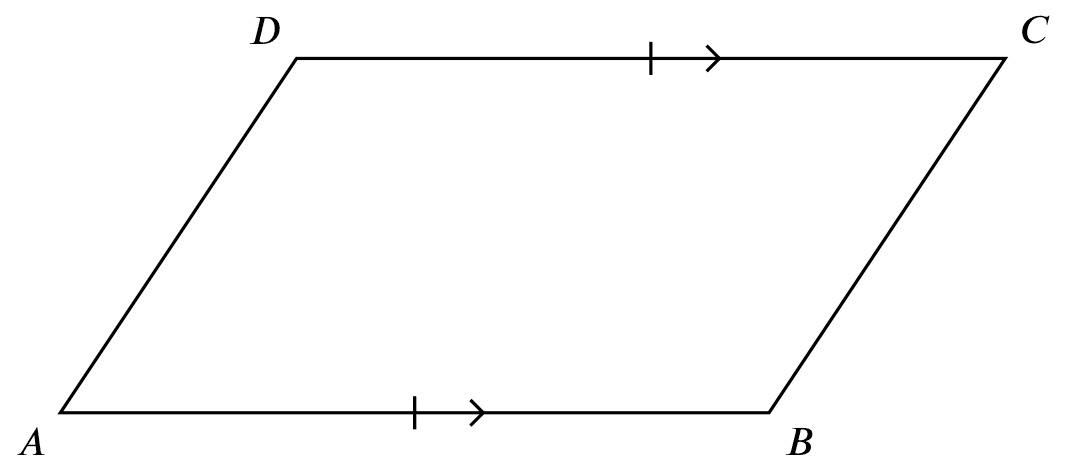
If

If $AB = DC$ and $DC \parallel AB$,

Then

$ABCD$ is a parallelogram

property of square

property of square

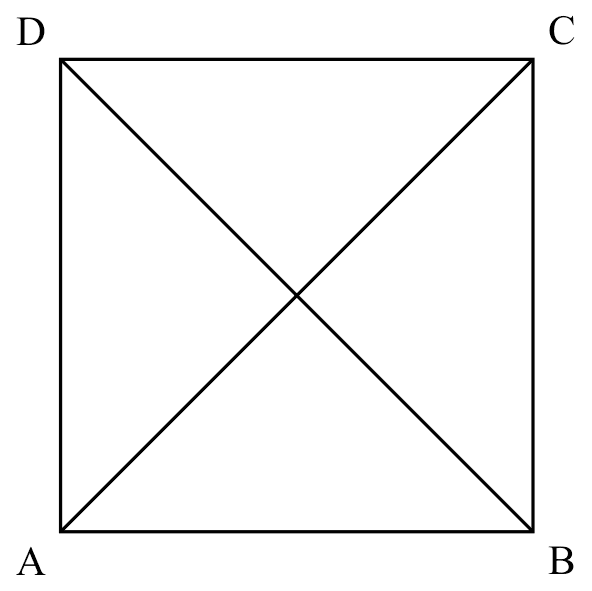
If

If $ABCD$ is a square,

Then

$AC=BD$

$AC \perp BD$

$\angle ADC= \angle DCB = \angle CBA = \angle BAD =90^{\circ}$

$AB=BC=CD=DA$

$DB$ bisects $\angle ABC$ and $\angle ADC$

$AC$ bisects $\angle DAB$ and $\angle DCB$

it posses all properties of a parallelogram

property of rectangle

property of rectangle

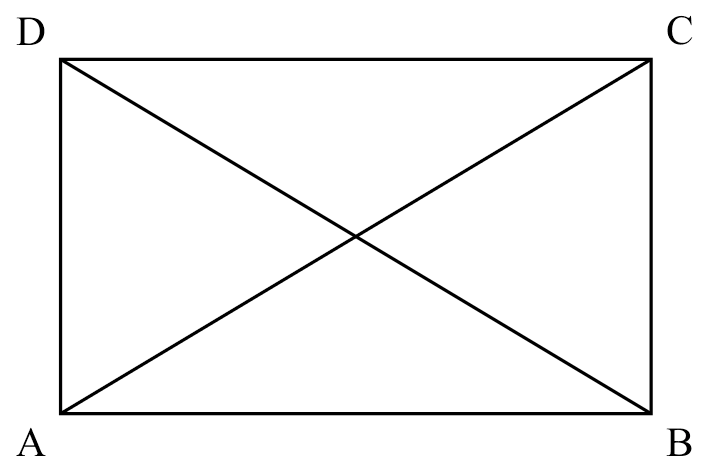
If

If $ABCD$ is a rectangle,

Then

$AC=BD$

$\angle ADC= \angle DCB = \angle CBA = \angle BAD =90^{\circ}$

it posses all properties of a parallelogram

property of rhombus

property of rhombus

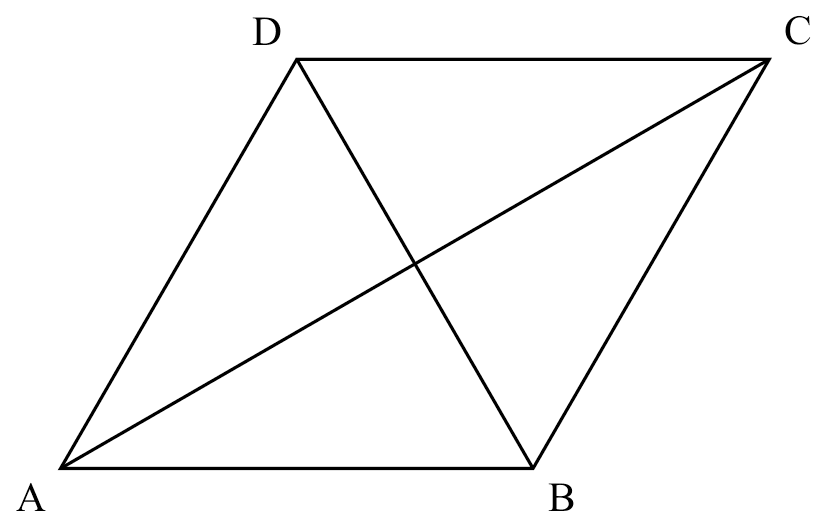
If

If $ABCD$ is a rhombus,

Then

$AB=BC=CD=DA$

$AC \perp BD$

$AC$ bisects $\angle BAD$ and $\angle BCD$

$BD$ bisects $\angle ABC$ and $\angle ADC$

it posses all properties of a parallelogram

property of kite

property of kite

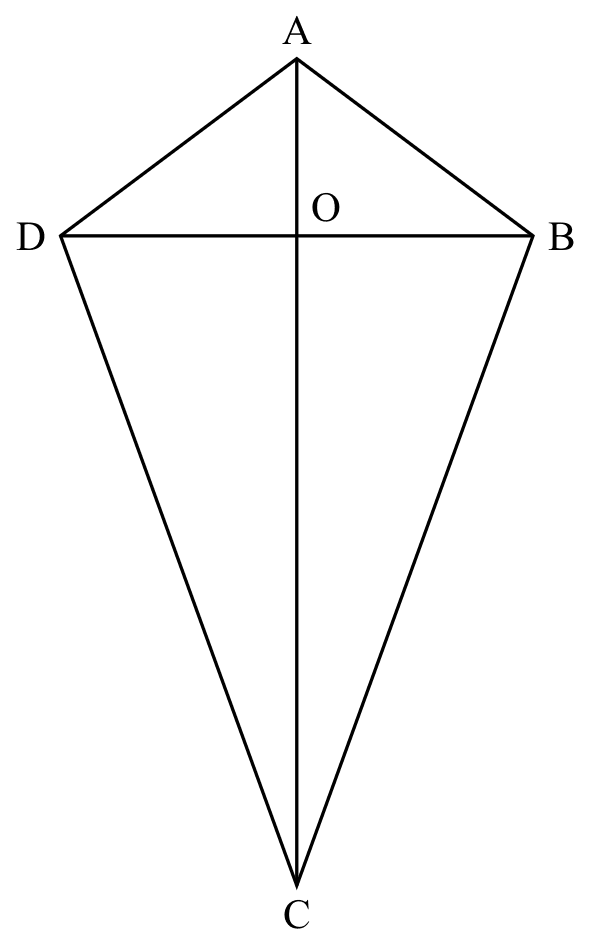
If

If $ABCD$ is a kite,

Then

$AC \perp BD$

$AD=DB$

$DC=BC$

$OD=OB$

$\angle DAO=\angle BAO$

$\angle DCO =\angle BCO$

property of trapezium

property of trapezium

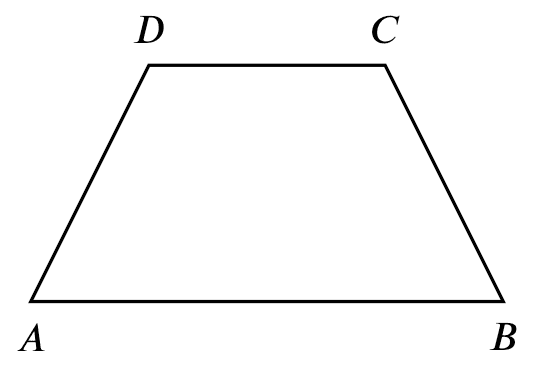
If

If $ABCD$ is a trapezium,

Then

$DC \parallel AB$

$\angle CDA + \angle DAB = 180^{\circ}$

$\angle DCB + \angle CBA = 180^{\circ}$

Circles

Let O be the centre of all the circles below.

21

line from centre $\perp$ chord bisects chord

$line from centre $\perp$ chord bisects chord$

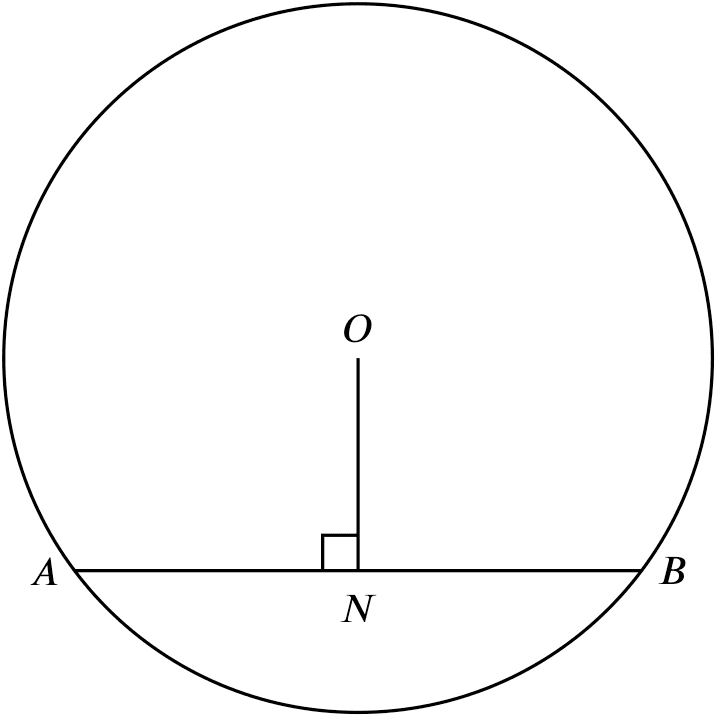
If

If $ON \perp AB$,

Then

$AN = NB$

line joining centre to mid-pt. of chord $\perp$ chord

$line joining centre to mid-pt. of chord $\perp$ chord$

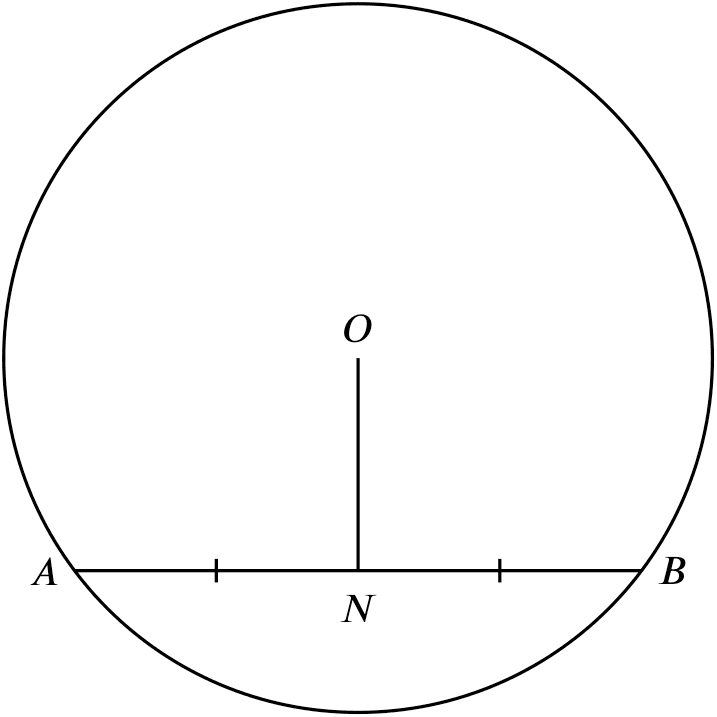
If

If $AN = NB$,

Then

$ON \perp AB$ ($\angle ANO$ and $\angle ONB = 90^{\circ}$)

$\perp$ bisector of chord passes through center

$$\perp$ bisector of chord passes through center$

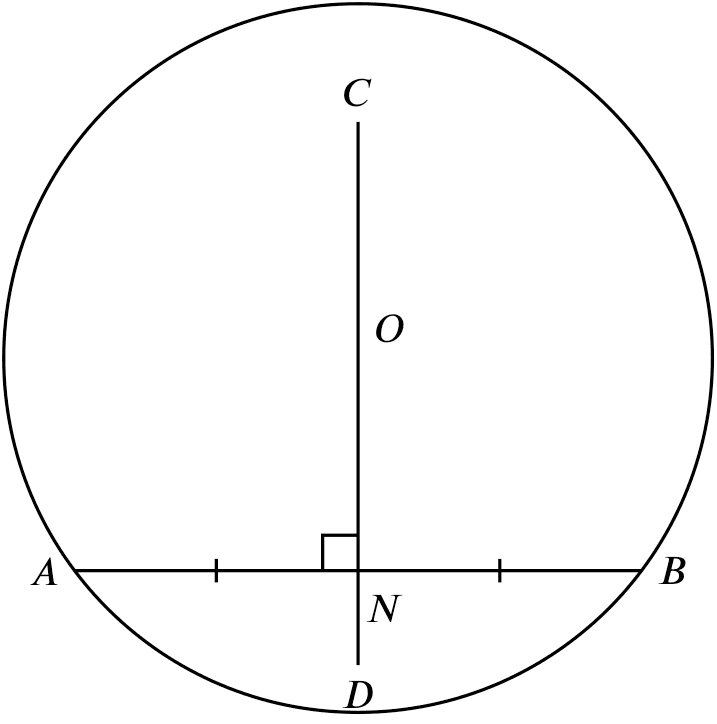
If

If $AN = NB$ and $CD \perp AB$,

Then

$CD$ passes through the center O

equal chords, equidistant from centre

equal chords, equidistant from centre

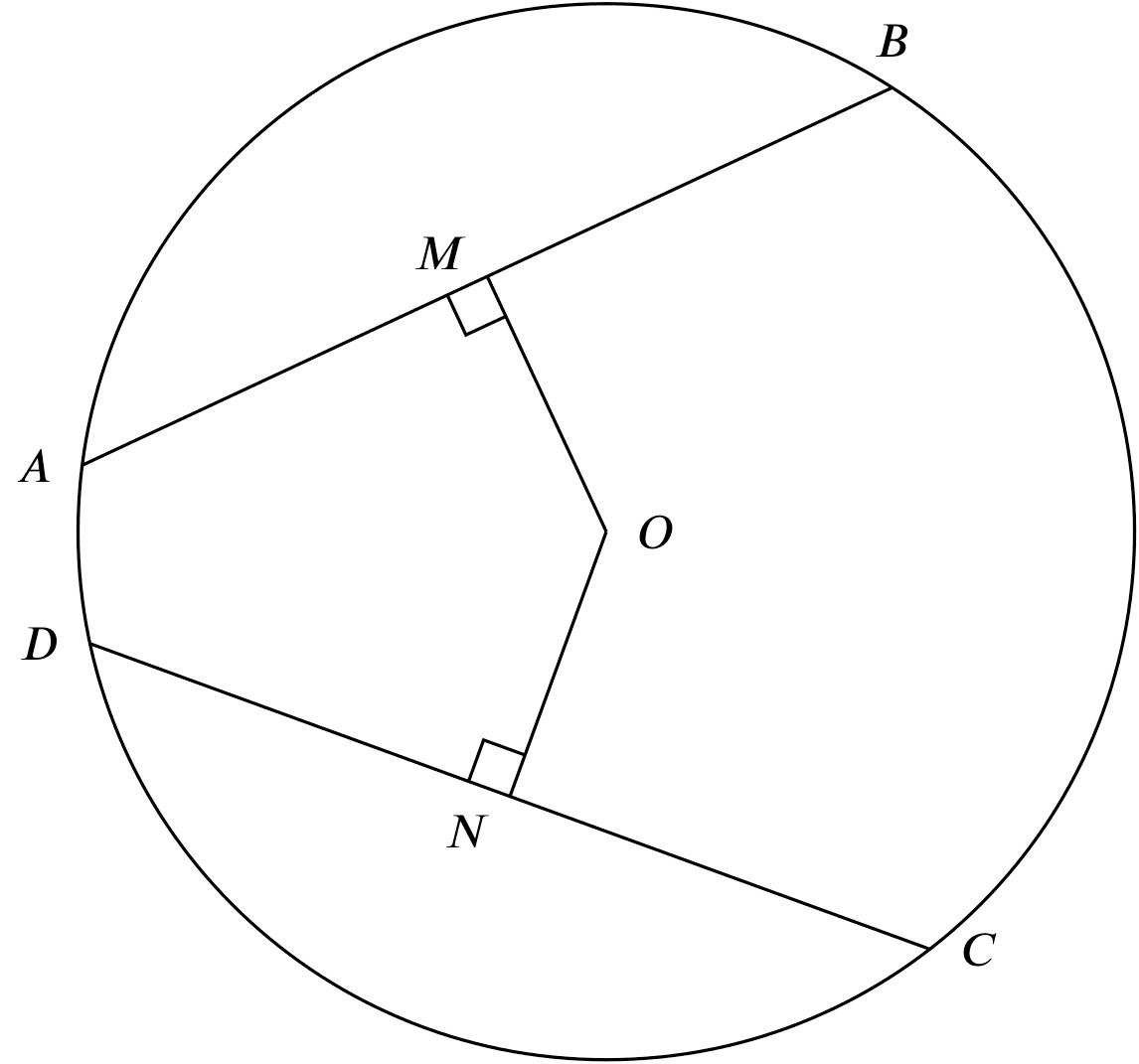
If

If $AB = CD$ and $OM \perp AB$ and $ON \perp CD$,

Then

$OM = ON$

chords equidistant from centre are equal

chords equidistant from centre are equal

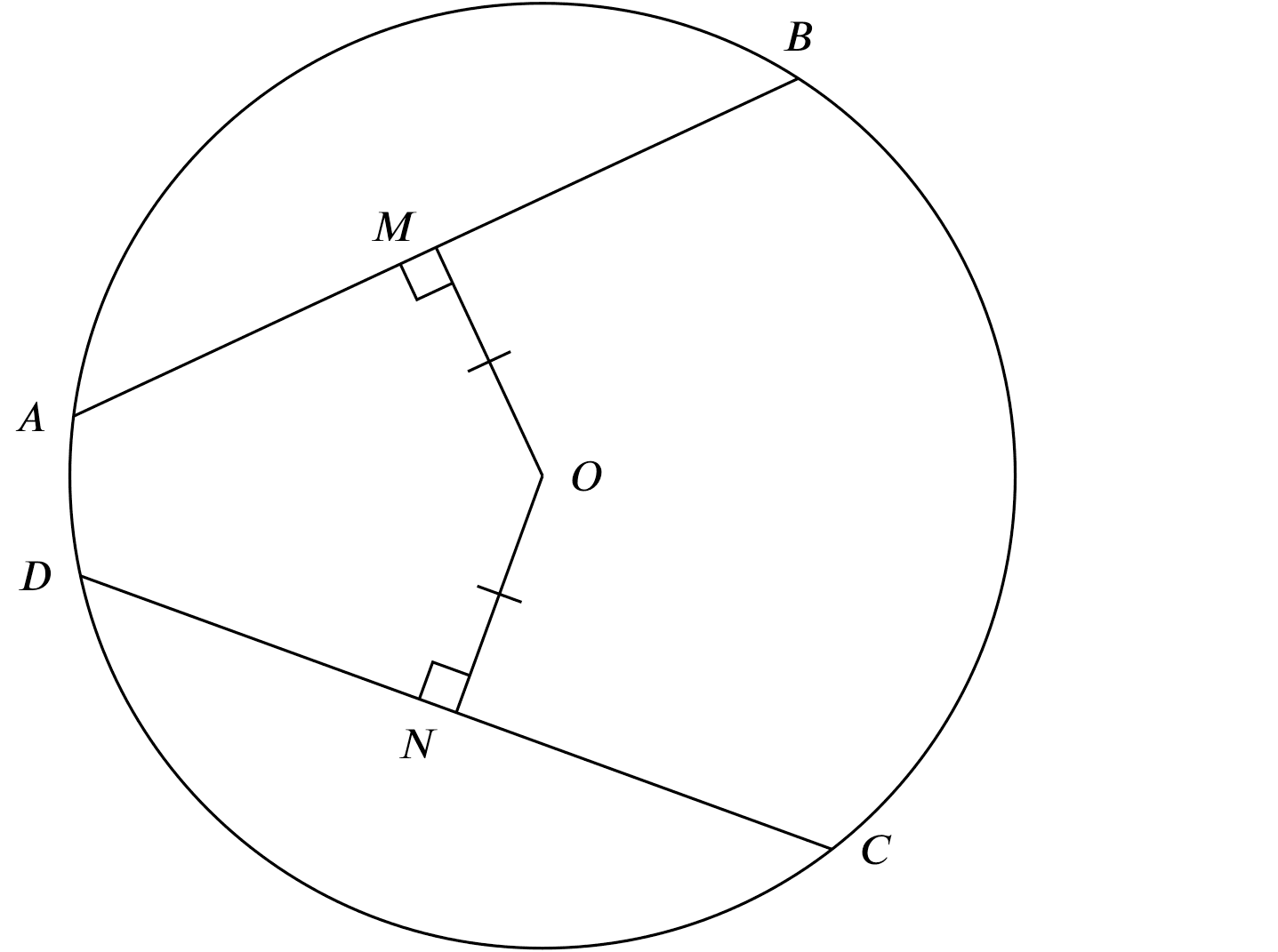
If

If $OM = ON$ and $OM \perp AB$ and $ON \perp CD$,

Then

$AB = CD$

$\angle$ at center twice $\angle$ at ☉$^{ce}$

$\angle$ at center twice $\angle$ at ☉$^{ce}$

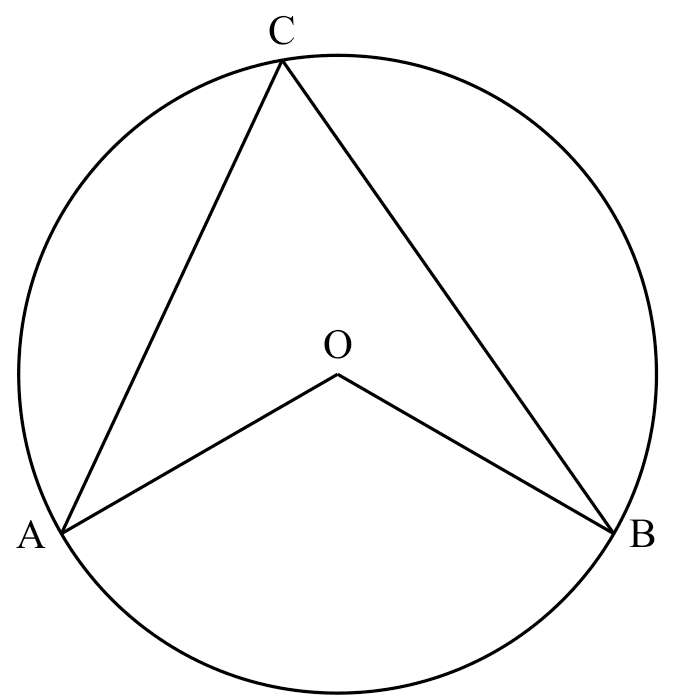
$\angle AOB = 2\,\angle ACB$

$\angle$ in semi-circle

$$\angle$ in semi-circle$

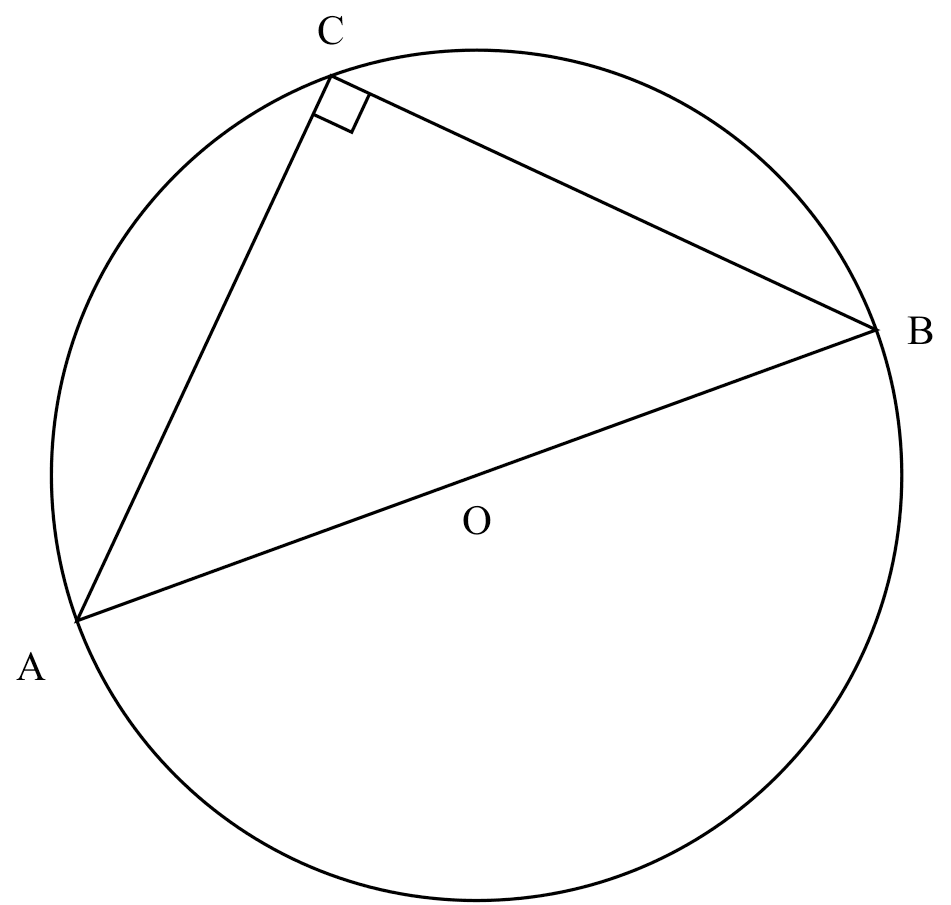
If

If AB is the diameter of the circle,

Then

$\angle ACB = 90^{\circ}$

$\angle$s in the same segment

$$\angle$s in the same segment$

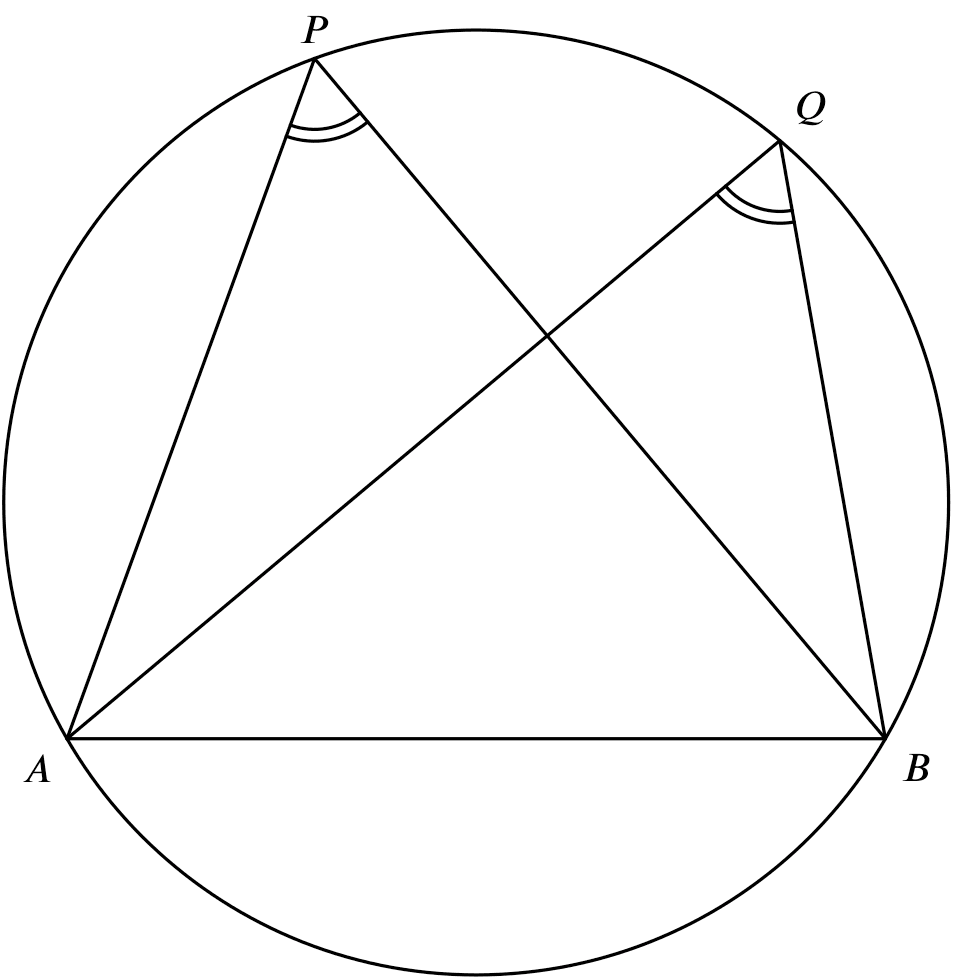
$\angle APB = \angle AQB$

arcs proportional to $\angle$s at centre

$arcs proportional to $\angle$s at centre$

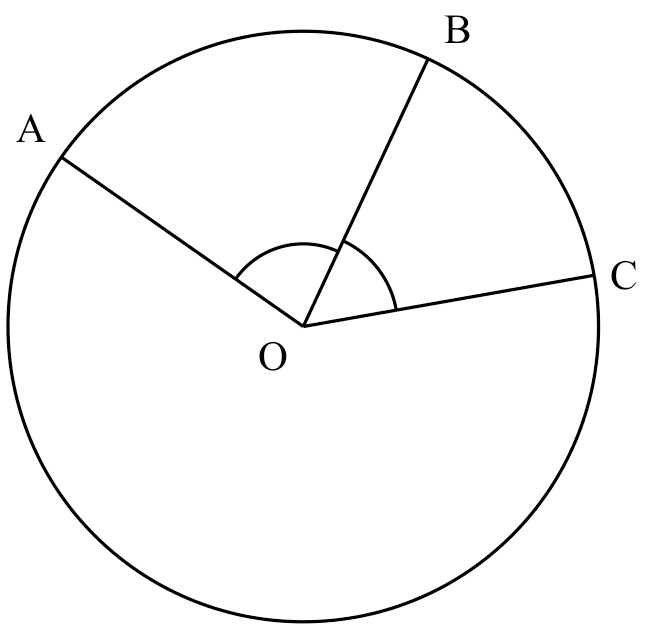
$\overset{\frown}{AB}: \overset{\frown}{BC}= \angle AOB : \angle BOC$

arcs proportional to $\angle$s at circumference

$arcs proportional to $\angle$s at circumference$

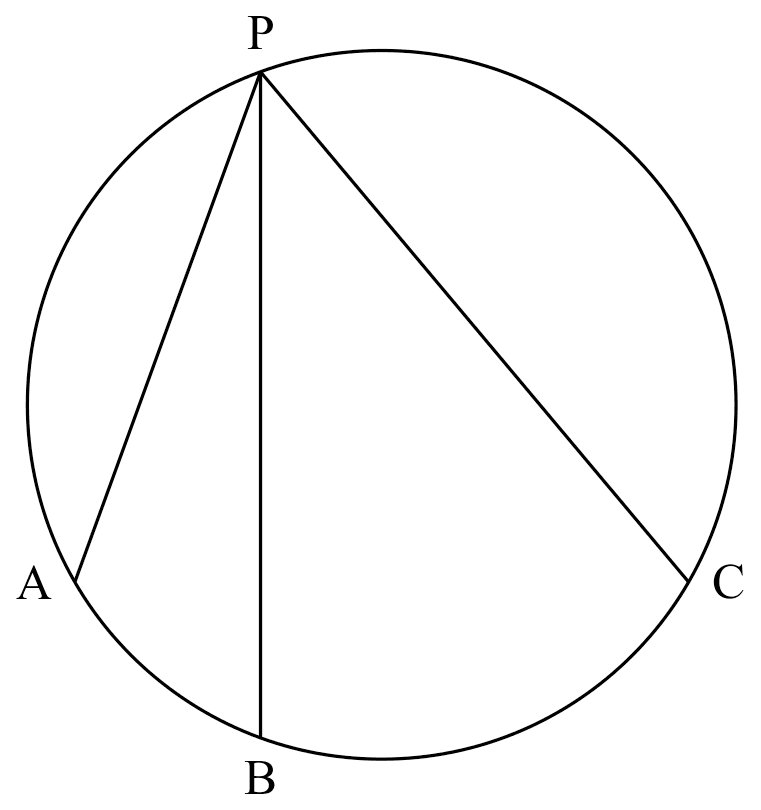
$\overset{\frown}{AB}: \overset{\frown}{BC}= \angle APB : \angle BPC$

equal chords, equal arcs

equal chords, equal arcs

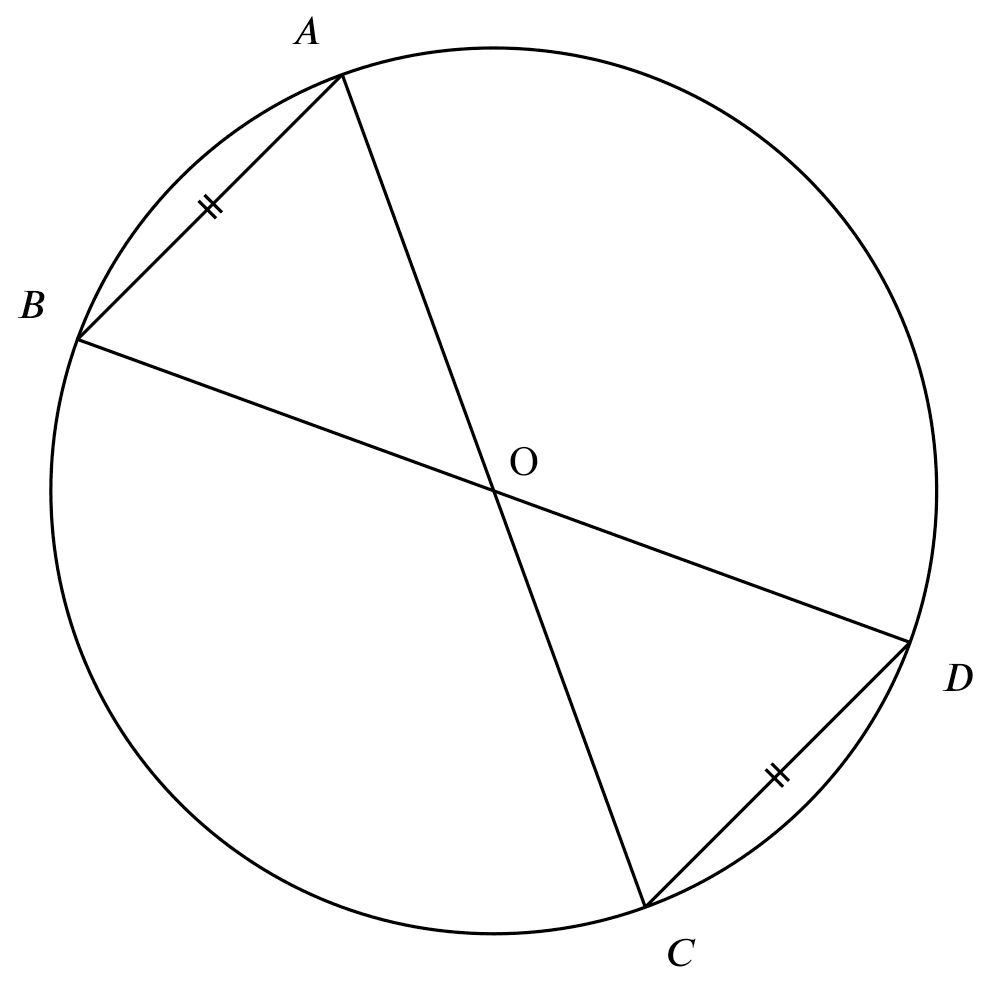
If

If $AB = CD$,

Then

$\overset{\frown}{AB}= \overset{\frown}{CD}$

equal arcs, equal chords

equal arcs, equal chords

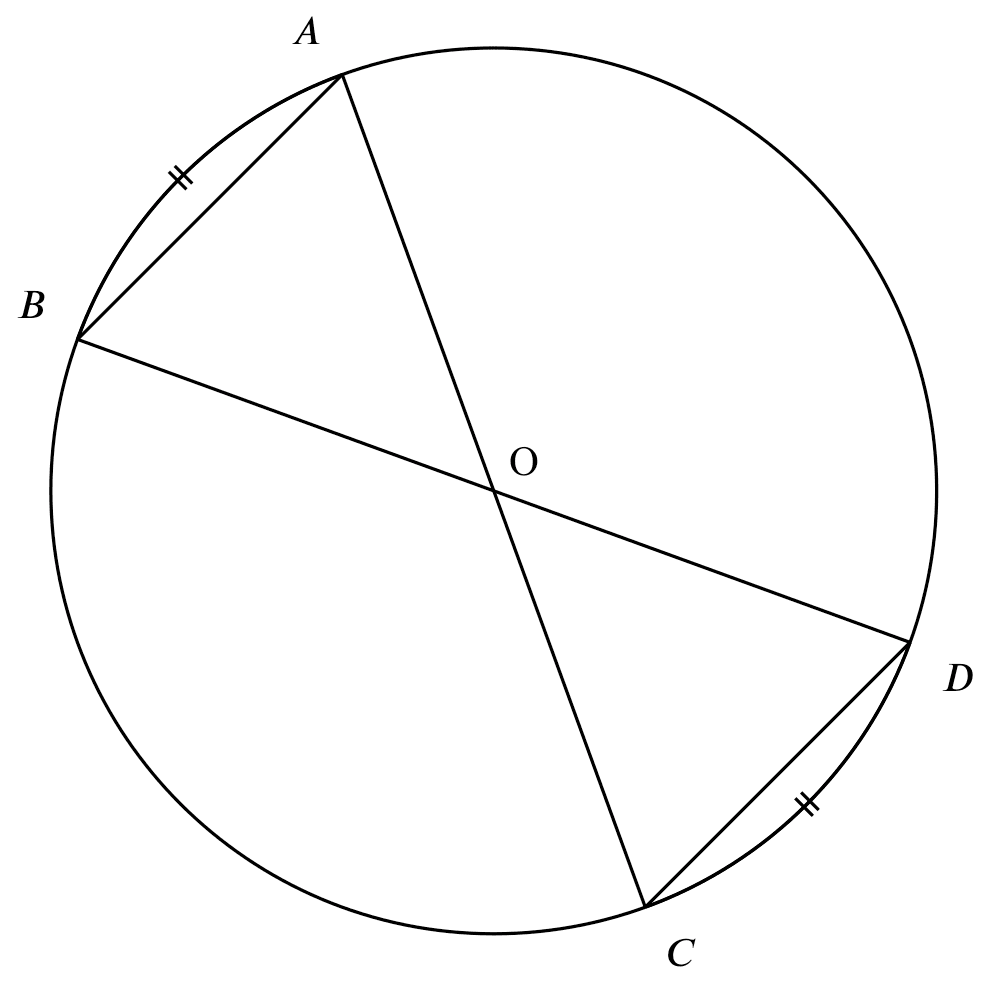
If

If $\overset{\frown}{AB}= \overset{\frown}{CD}$,

Then

$AB = CD$

equal arcs, equal $\angle$s

$equal arcs, equal $\angle$s$

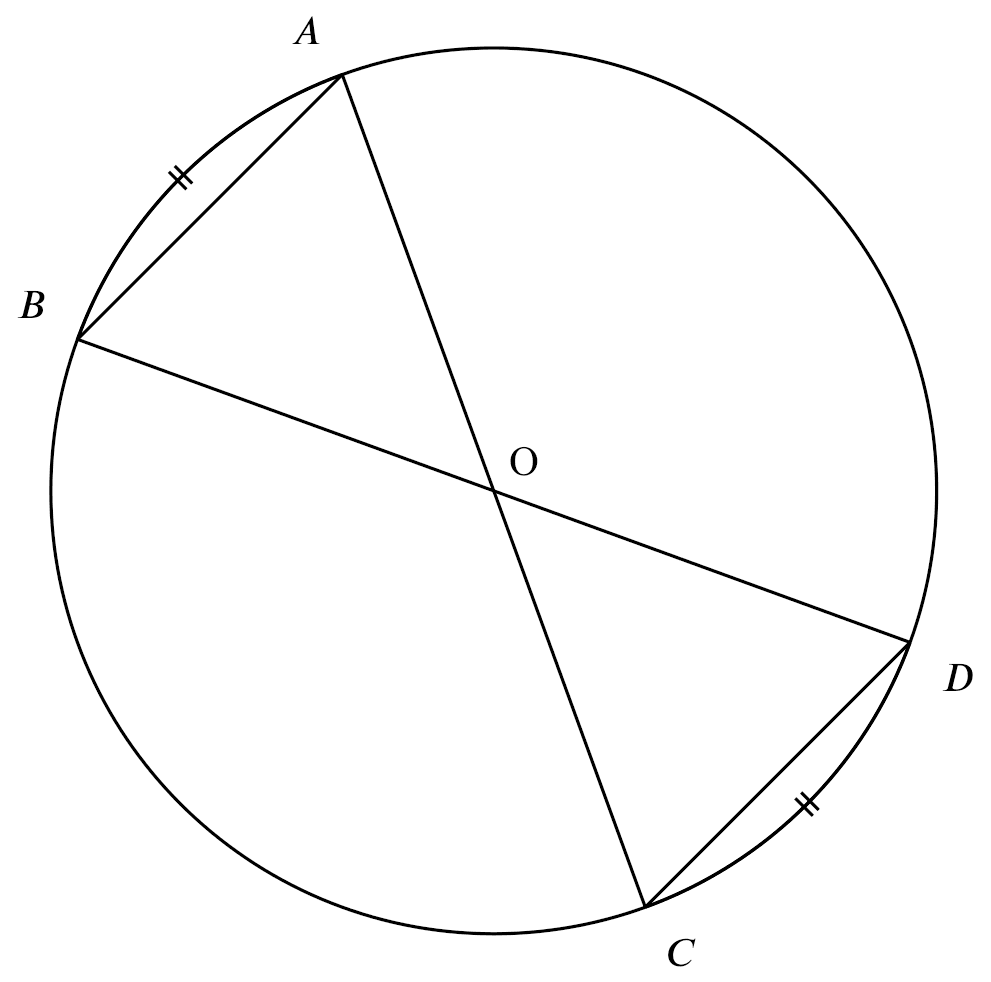
If

If $\overset{\frown}{AB}= \overset{\frown}{CD}$,

Then

$\angle AOB = \angle COD$

equal $\angle$s, equal arcs

$equal $\angle$s, equal arcs$

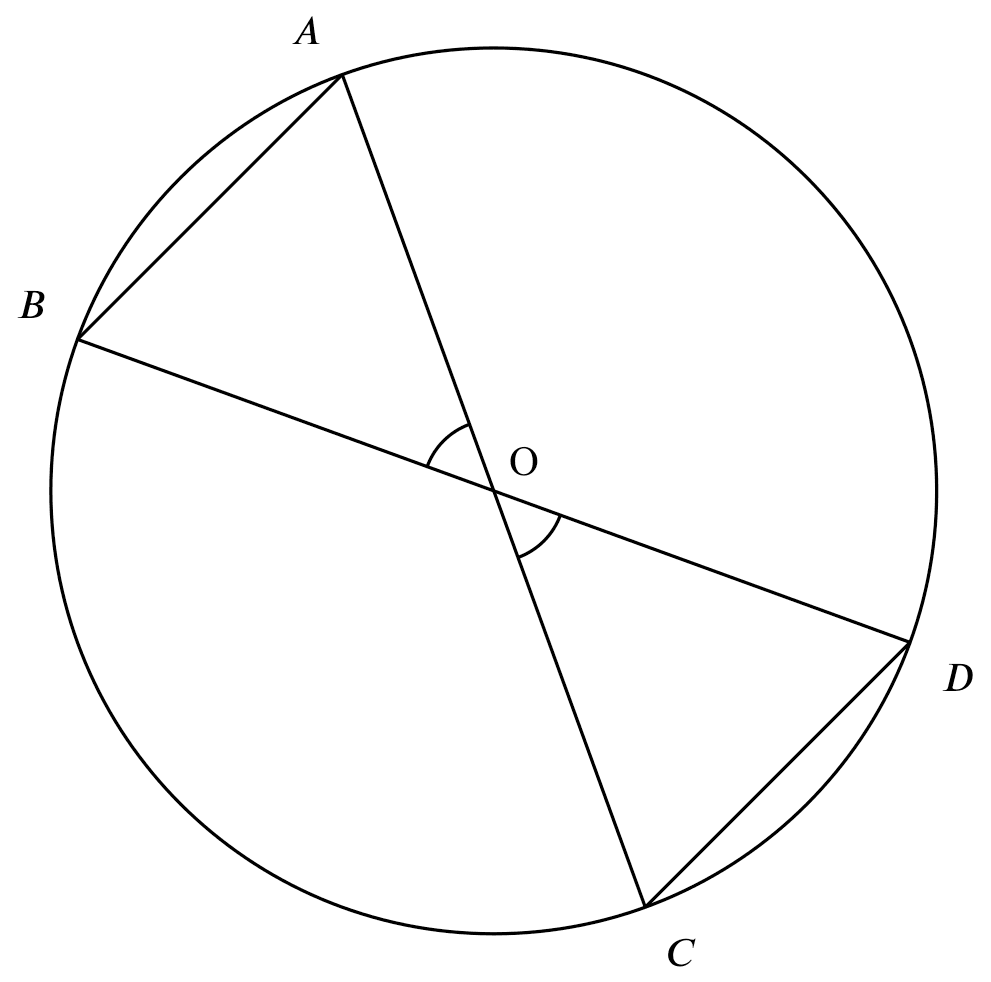
If

If $\angle AOB = \angle COD$,

Then

$\overset{\frown}{AB}= \overset{\frown}{CD}$

equal chords, equal $\angle$s

$equal chords, equal $\angle$s$

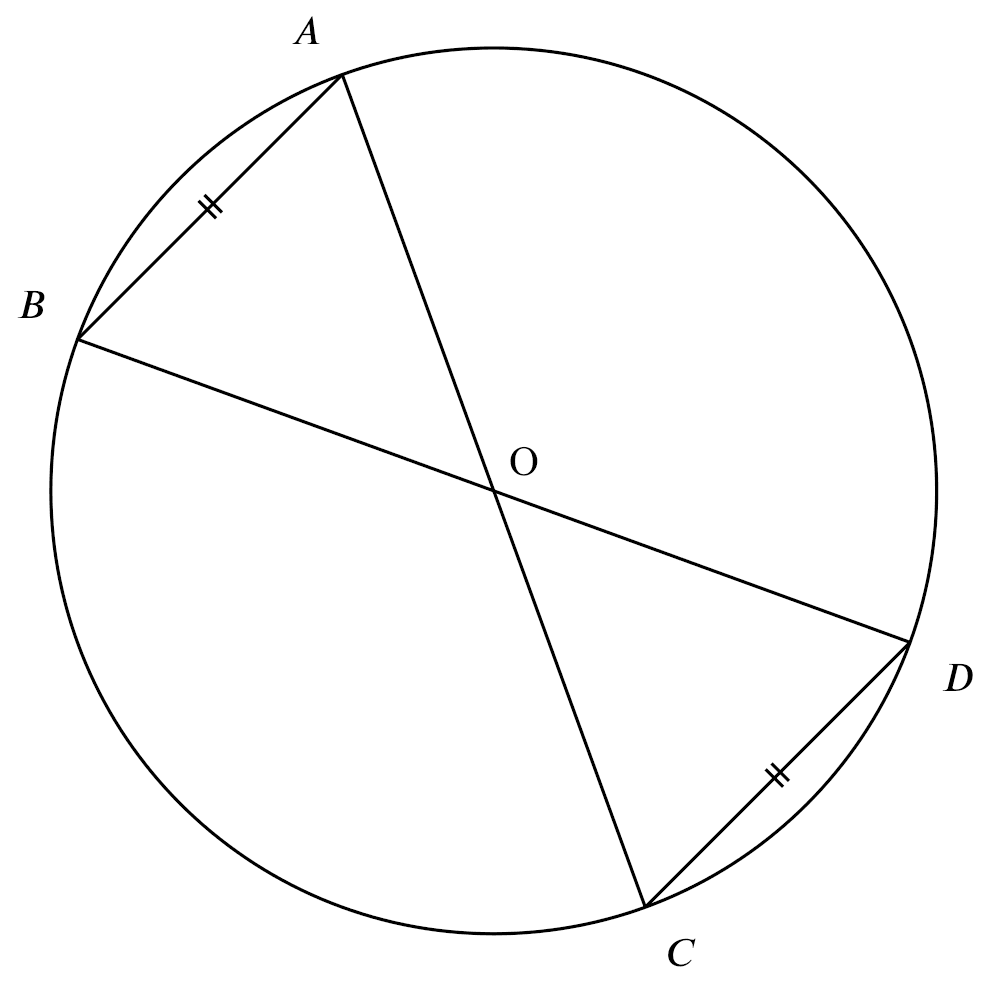
If

If $AB = CD$,

Then

$\angle AOB = \angle COD$

equal $\angle$s, equal chords

$equal $\angle$s, equal chords$

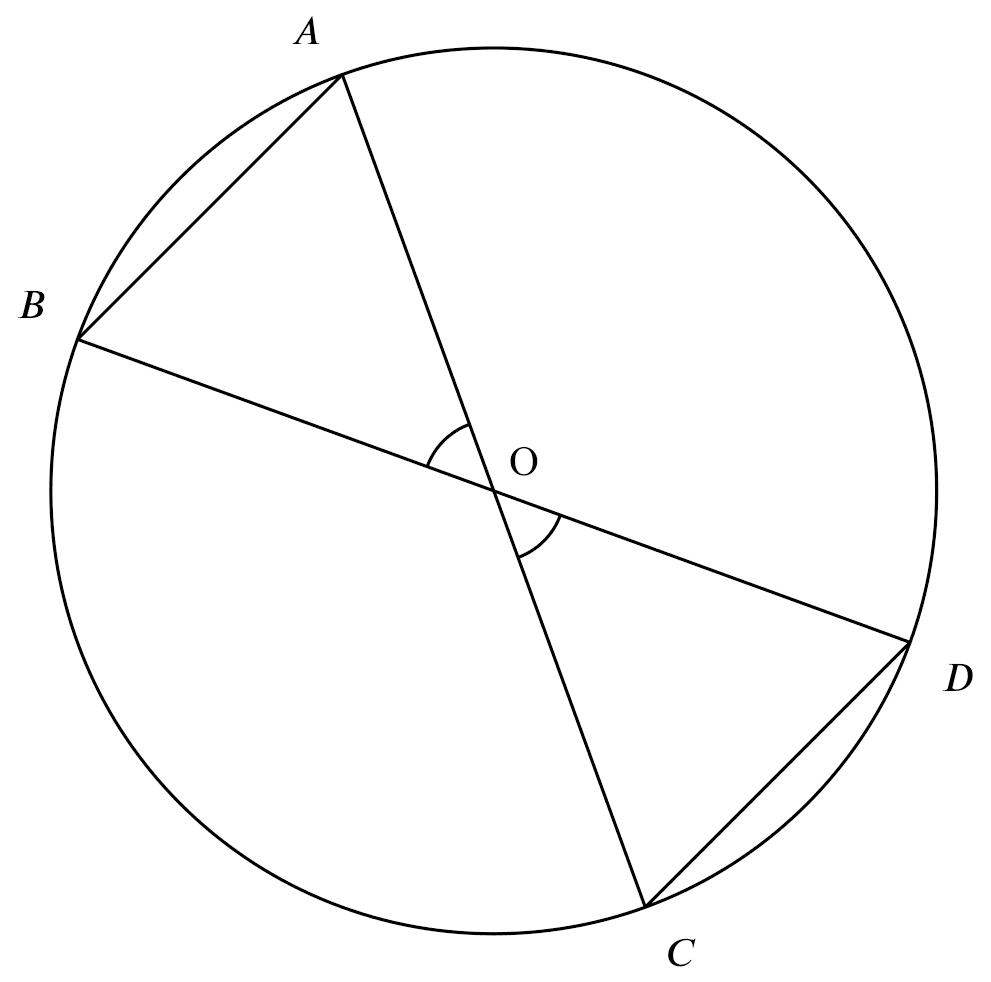
If

If $\angle AOB = \angle COD$,

Then

$AB = CD$

opp. $\angle$s, cyclic quad.

$opp. $\angle$s, cyclic quad.$

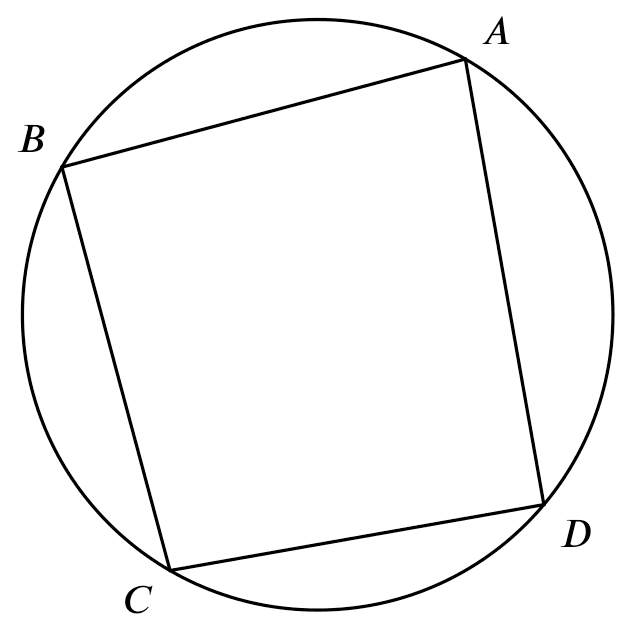
If

If $ABCD$ is a cyclic quadrilateral,

Then

$\angle ABC + \angle ADC = 180^{\circ}$

$\angle BAD + \angle BCD = 180^{\circ}$

ext. $\angle$s, cyclic quad.

$ext. $\angle$s, cyclic quad.$

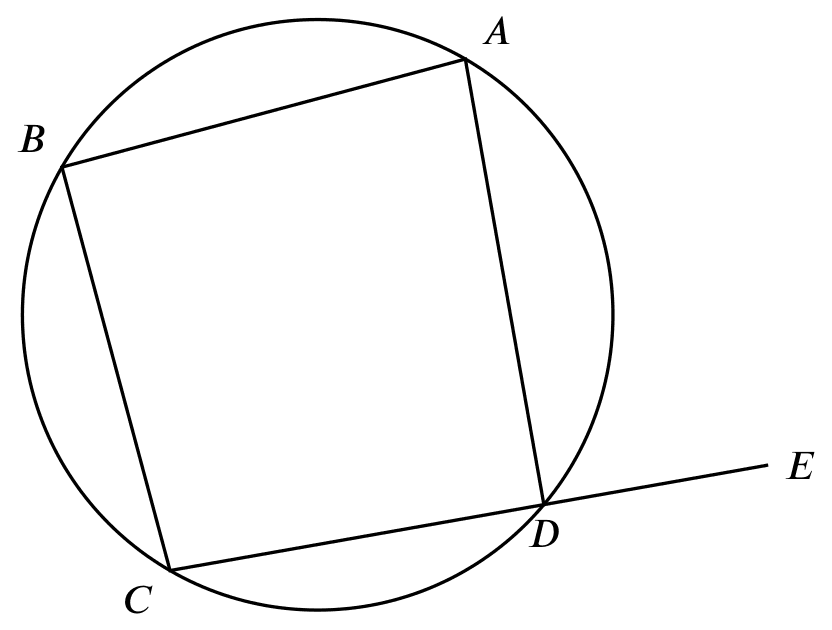
If

If $ABCD$ is a cyclic quadrilateral,

Then

$\angle ABC = \angle ADE$

converse of $\angle$s in the same segment

$converse of $\angle$s in the same segment$

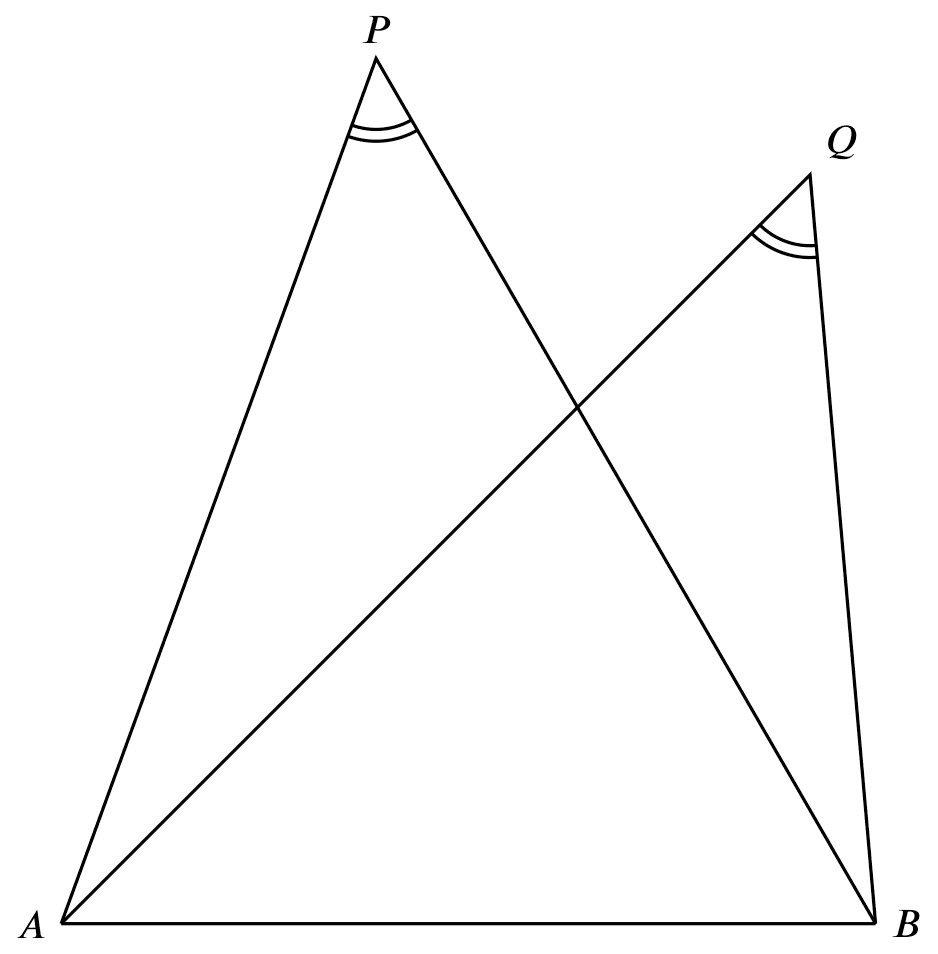
If

If $\angle APB = \angle AQB$,

Then

A,B,Q,P are concyclic

opp. $\angle$s supp.

$opp. $\angle$s supp.$

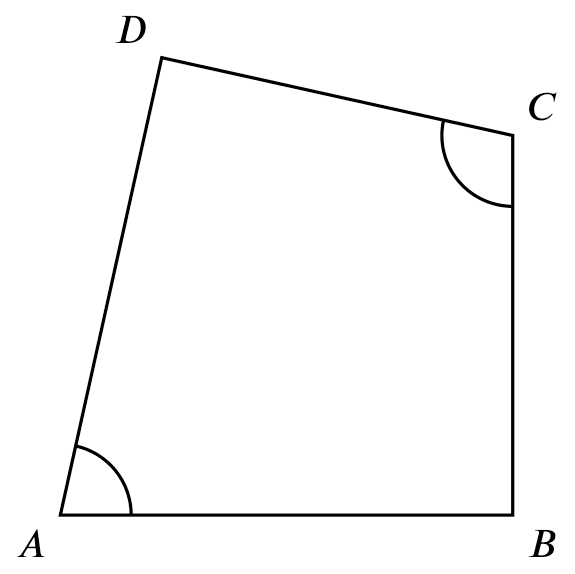
If

If $\angle DAB + \angle BCD = 180^{\circ}$,

Then

$ABCD$ are concyclic

ext. $\angle$ = int. opp. $\angle$

$ext. $\angle$ = int. opp. $\angle$$

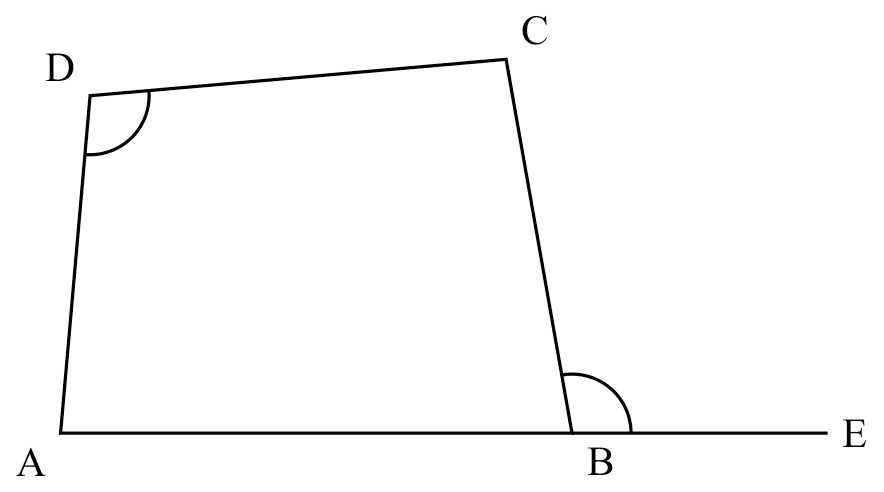
If

If $\angle ADC = \angle CBE$,

Then

$ABCD$ are concyclic

Tangents

5

tangent $\perp$ radius

$tangent $\perp$ radius$

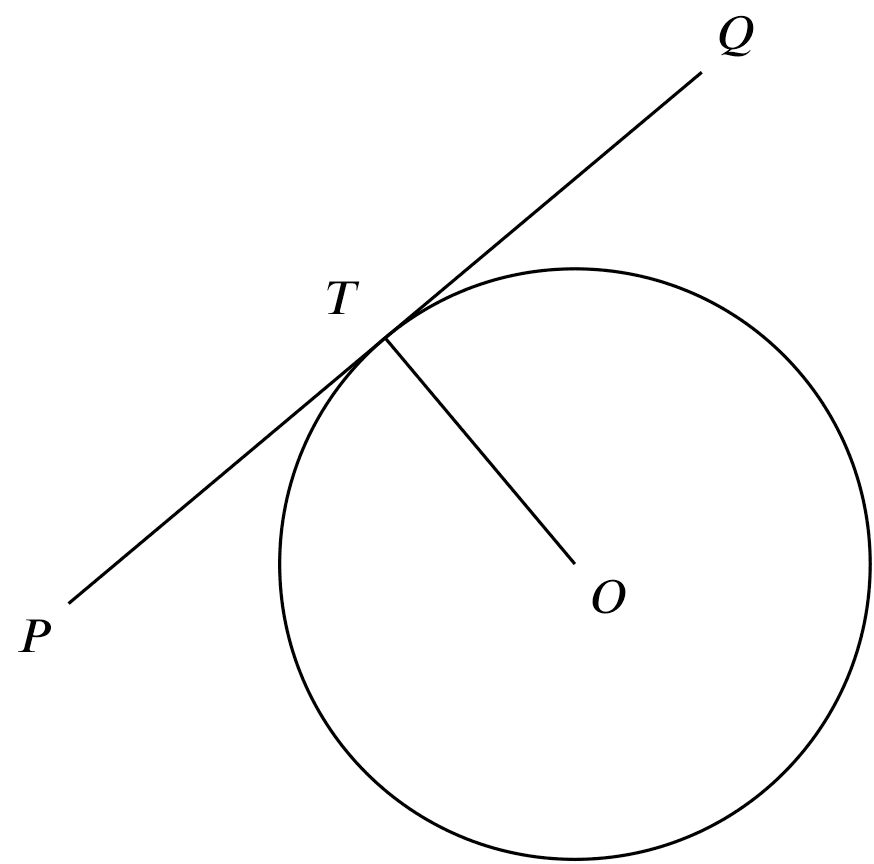
If

If PQ is tangent at T,

Then

$PQ \perp OT$

converse of tangent $\perp$ radius

$converse of tangent $\perp$ radius$

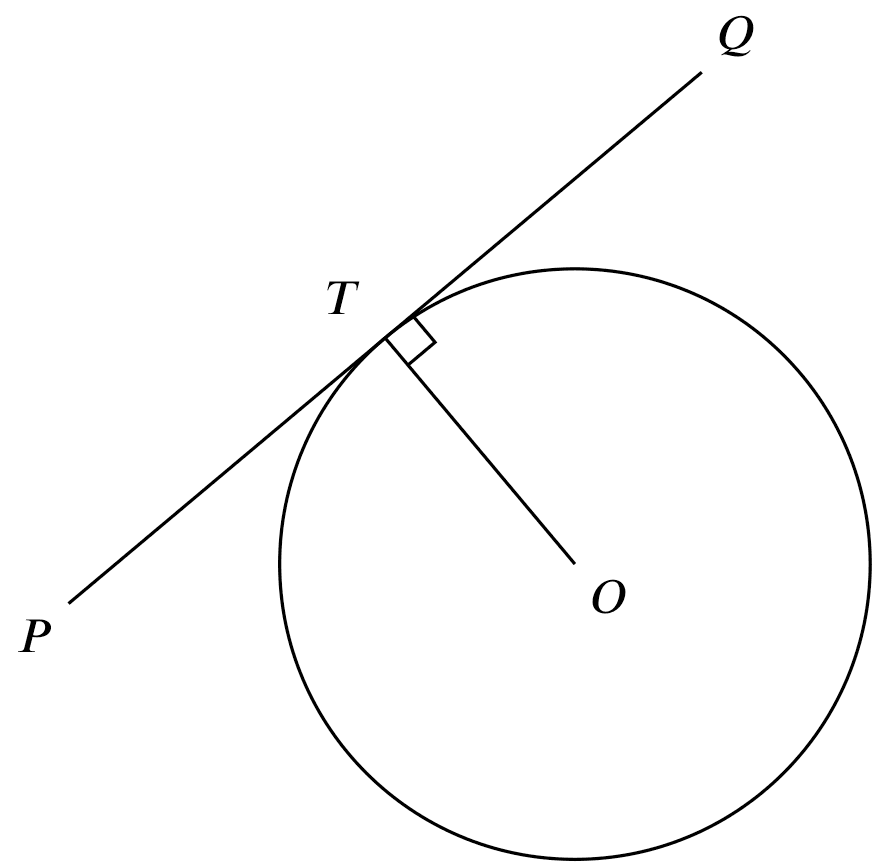
If

If $OT \perp PQ$,

Then

$PQ$ is tangent at T

tangent properties

tangent properties

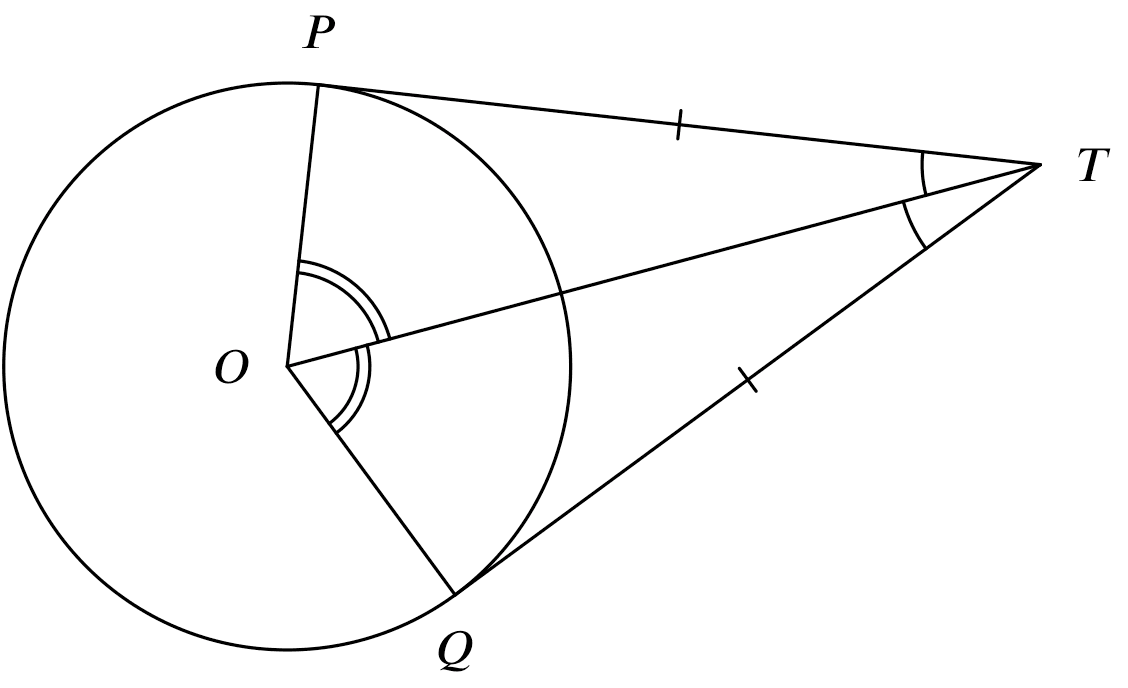
If

If TP and TQ are tangents at P and Q from T,

Then

$\angle TOP=\angle TOQ$

$\angle OTP=\angle OTQ$

$TP= TQ$

$\angle$s in alt. segment

$$\angle$s in alt. segment$

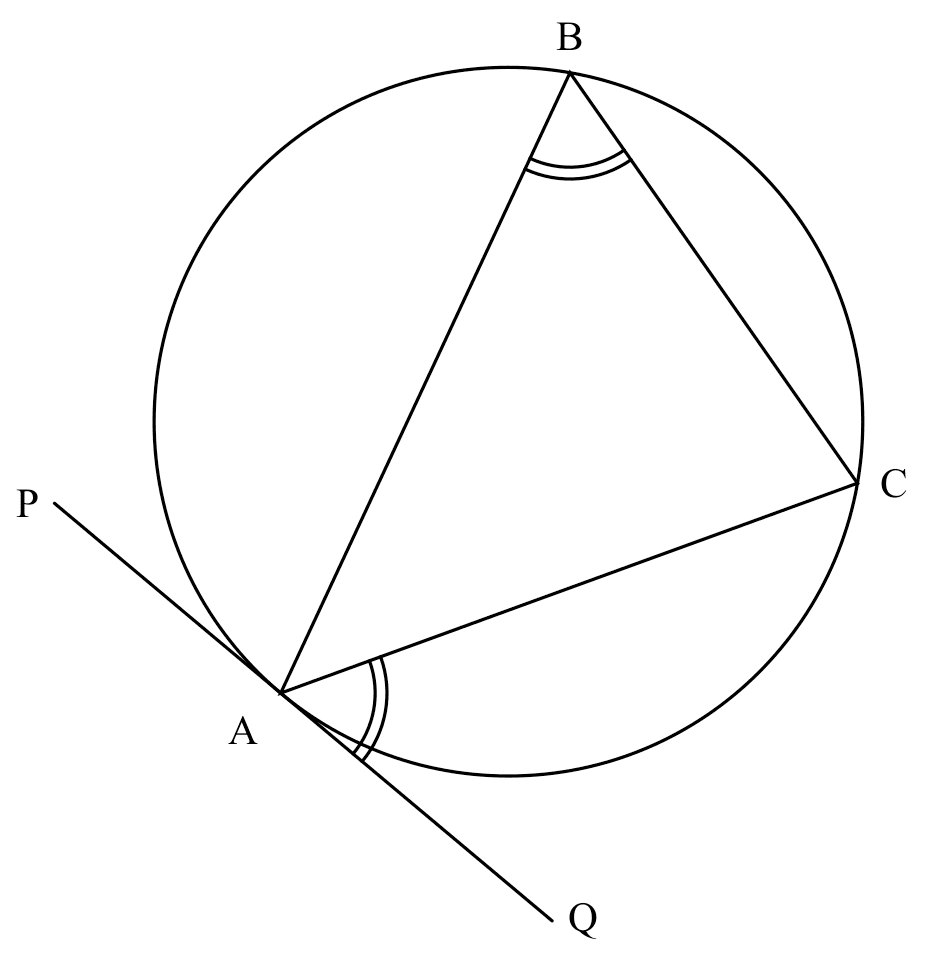
If

If PQ is tangent at A,

Then

$\angle QAC = \angle ABC$

converse of $\angle$s in alt. segment

$converse of $\angle$s in alt. segment$

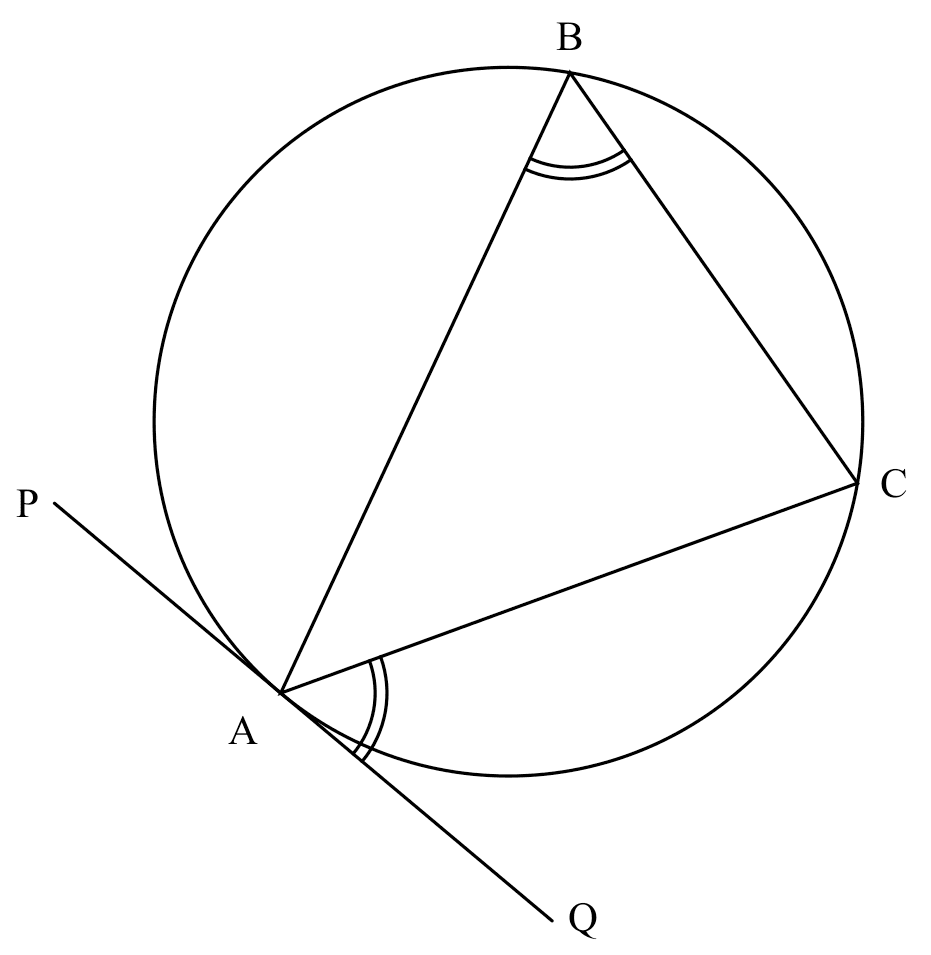
If

If $\angle QAC = \angle ABC$,

Then

$PQ$ is tangent at A

HKDSE Geometry Reasons Cheat Sheet | Complete Revision Guide